1

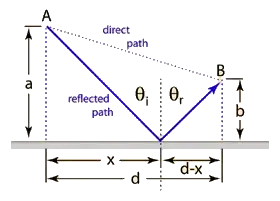
In our textbook, it's written that light rays will follow the minimum or maximum distance after being reflected from the plane surface and thus the path will be fixed.

At somewhere, I read that light would follow all possible ways. But in this case, the probability of those unlikely paths gets cancelled. Maybe, it could be the selection of nature of Quantum Mechanics says something different but still I don't know.

If we consider point '$A$' as the source of light, then at a point '$O$' (not mentioned in the following figure), light drops on the mirror and then is reflected towards point '$B$'. Then we can possibly notify the whole path as $AOB$ = $s$

Fermat's Principle about 'Laws of Reflection'

Now Fermat's principle is saying that '$s$' would be the maximum or minimum for the light's trajectory showing the equation $$ \frac {ds}{dx} = 0$$

It seems a bit confusing to me because all I knew is that light follows the way it takes least time to travel.

So, what's the logic behind the longest way? Can we lead any conclusion anyhow with the term $ \frac {ds}{dx} = 0$ for defining it?

Qmechanic
  • 220,844

1 Answers1

0

I think what are you looking at is still the shortest path for a ray that reflects from the mirror. We can easily imagine a second mirror which can reflect a ray from A to B but for which the light's trajectory is any arbitrary value ...

Truth_Seeker
  • 1