1

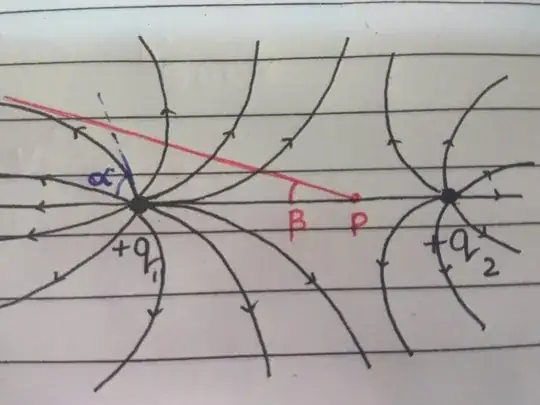
For two positive point charges in space separated by some finite distance, the electric field lines we observe look like this:

(for point $P$ being the neutral point, the line shown in red is asymptotic to the field line emerging from a charged point $q_{_1}$ at an angle $\alpha$)

Suppose we have 2 positive charges $q_{_1}$ and $q_{_2}$. If an electric field line emerges from $q_{_1}$ at an angle $\alpha$ from the line joining charges $q_{_1}$ and $q_{_2}$, is there a way we can derive the slope of asymptote to the given field line?

In simple words, can we derive a relationship between $\alpha$ and $\beta$?

Edit

I've been thinking that if somehow we can count the number of field lines emitted in the conical region, having semi vertical angle equal to $\beta$ and with its vertex at $P$, that do not go out of the curved surface area of the cone (hence I mean, measuring the flux through the base of the cone); we can then equate this with the number of field lines emitted from charge $q_{\small{1}}$ within the solid angle $ \Omega= 2\pi\left(1- \cos(\alpha)\right)$. Which is, in magnitude, equal to $\varphi=\frac{q_{\small{1}}}{2\varepsilon_0}\left(1-cos\alpha\right)$.

Hence my question shrinks to:

  • How to calculate the number of field lines emitted inside the solid angle $2\pi\left(1-\cos\beta\right)$ subtended at point $P$?
Emilio Pisanty
  • 137,480
SteelCubes
  • 465

2 Answers2

2

The arguments regarding the conservation of electric flux in this previous answer of mine apply equally well here, with the minor change that the second angle corresponds to the combined charges here: the flux calculation happens, asymptotically, at infinity, where the electric field looks like that of a point charge with the combined charge, located at the center of charge (as defined here), plus a quadrupole correction which is negligible at infinity.

As such, the correct relationship between the two angles, as you have defined them, is $$ (1-\cos(\alpha))q_1 = (1-\cos(\beta))(q_1+q_2). $$

Emilio Pisanty
  • 137,480
0

Going with Michael's idea and noting that the field line of interest in your sketch is actually the resultant field, then at very large distances the asymptote becomes a tangent to a radial resultant from a net charge q = $q_1$ + $q_2$. Then the number you are looking will be the total number of lines times the fraction of a sphere occupied by the given solid angle; N = (lines/coulomb)q[Ω/(4π)].

R.W. Bird
  • 12,280