Generally speaking, yes -- for a fixed angle of attack, increasing the velocity will cause separation to occur earlier. It is not quite that simple, because flow regimes will change at certain speeds and alter the process (for example, laminar to turbulent or incompressible to compressible), but let's break it down.
We can start by looking at what happens in very, very slow flows. These are commonly called Stokes flow, or creeping flows. Under these conditions, the pressure gradients are very small and the only forces that really act on the fluid are viscous forces. Under this regime, there is no flow separation from the air foil, even for large angles of attack. The flow stays attached and moves smoothly over the body.
When the flow velocity starts to increase, we now start to get an increased importance of the pressure gradient forces on the flow. Let's think about the fluid particle as it is moving towards the leading edge of the airfoil... As it approaches the airfoil, it is going to start to feel the influence of the airfoil and start to move up or down to go around the body. Let's follow a particle that is moving over the top surface of the airfoil.
As the fluid particle starts to move over the leading edge, it starts to feel a contraction in the flow area. Since the flow is subsonic, this contraction in flow area leads to an acceleration of the fluid particle as it moves along the leading edge of the airfoil. If we were to measure the pressure along the airfoil leading edge, the pressure is decreasing as we move along the surface. The particle is experiencing a favorable pressure gradient and accelerating.
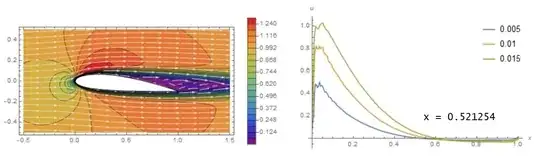
Once it gets to the top of the airfoil, it sees an expansion of the flow area. For a subsonic flow, this causes it to slow down. If we think again in terms of pressure along the top surface, the pressure is higher at the tail end of the top surface than it is at the leading edge of the top surface. The fluid particle feels an adverse pressure gradient slowing it down.
As the flow speeds increase, the pressure difference between the leading edge of the top surface and the tail of the top surface becomes larger. Since the airfoil is always the same length, a bigger pressure difference over the same distance is a stronger pressure gradient. And since the pressure is increasing along the surface, it is an adverse pressure gradient.
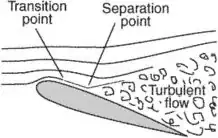
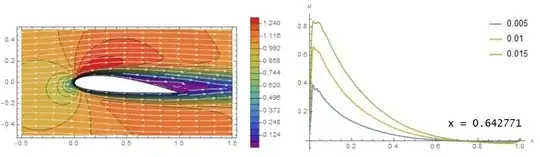
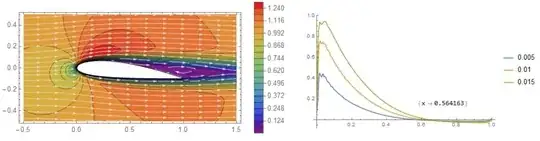
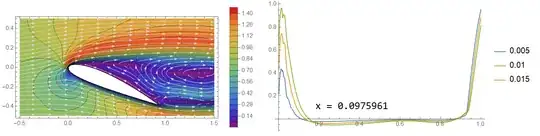
At some flow speed, this gradient will become strong enough to cause the fluid parcel moving along the top surface to stop completely before reaching the tail of the airfoil. This is when the flow separates. Going faster and faster will cause the separation point to happen sooner along the distance because the pressure gradient is stronger (and so the force slowing down the fluid particle is stronger).
That's the simplified overview of the process, but reality isn't as clear cut as that always. There are also going to be changes in flow regimes that may delay the separation point before it starts to move forward again.
For example, starting from very low speed flow and gradually increasing the speed, you may see separation start before turbulence begins to happen. This laminar separation point may move further up the surface of the airfoil until you reach a speed where now the boundary layer starts to be turbulent instead of laminar. This turbulent boundary layer may then reattach and you'll have a range of speeds, faster than ones that showed separation, where the flow stays attached.
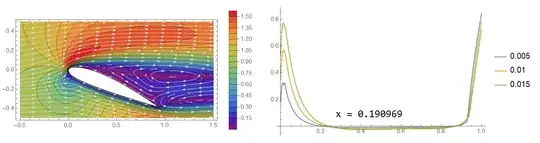
If you keep speeding up, even the turbulent boundary layer may start to separate. And as you speed up more, that separation point will start to happen earlier. But then you might be getting fast enough that compression and shocks start to form, and now you're in yet another flow regime that will change the behavior.
It's likely that if you get to the point shocks are forming, the flow will separate wherever the shock is sitting. It might reattach, or it might separate and stay separated. If your shock is at the leading edge, you might have separated flow over the entire body of the airfoil for all speeds beyond that point.
Because there seems to be a lot of misunderstanding of the physics going on here, let's take a look at the momentum equation along the top surface of the airfoil under steady, incompressible conditions:
$$ \frac{\partial u}{\partial s} = -\frac{1}{\rho} \frac{\partial P}{\partial s} + \frac{1}{\text{Re}} \frac{\partial^2 u}{\partial n^2} $$
where $s$ is the coordinate along the top surface, $n$ is the direction normal to that top surface, $\text{Re} = u L / \nu$ is the Reynolds number. The pressure gradient is proportional to $u^2$ (the dynamic pressure) and the Reynolds number is obviously linear in $u$.
At very very low speeds, the Stokes flow regime, $\text{Re} << 1$ and the viscous term dominates completely. This regime shows no flow separation.
However, because $P \propto u^2$ and the viscous terms scale independent of $u$ (i.e. $1/\text{Re}\,\partial^2 u/\partial n^2 \propto 1$), as the speed increases, the pressure gradient becomes dominant relatively quickly. Because the pressure gradient continues to increase in this regime while the viscous terms remain relatively stable, this is what leads the Wikipedia page on flow separation mentioned in the comments to note:
... the separation resistance of a laminar boundary layer is independent of Reynolds number — a somewhat counterintuitive fact.
So now let's move on to a turbulent, subsonic boundary layer. In this case, the viscous term becomes more complicated because of the Reynolds stress tensor and it is no longer independent of velocity. However, the pressure term still is $P \propto u^2$ while the viscous term is proportial to something less (if I remember correctly, it is proportional to velocity to a fractional power less than one, but I can't find it in my notes).
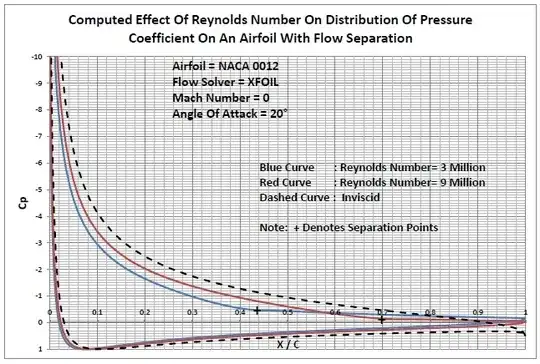
This means increasing speed will increase the pressure gradient, and the pressure gradient term is of leading order, $\partial P/\partial s >> \frac{1}{Re} \partial^2 u /\partial n^2$. So increasing speed increases adverse pressure gradients, which can move the separation point forward on the upper surface.
Again returning to the comments and to Wikipedia:
A secondary influence is the Reynolds number. For a given adverse $du_o/ds$ distribution, the separation resistance of a turbulent boundary layer increases slightly with increasing Reynolds number.
The key to that statement is that $du/ds$ is given. But $\partial u/\partial s$ is not constant if you take a fixed geometry and a fixed working fluid and speed up -- $\partial u/\partial s \propto \partial P/\partial s \propto u^2$. The only way to increase Reynolds number while holding $\partial u/\partial s$ constant is to change the working fluid or change the body shape.
All together, this means for a subsonic flow, there are two regimes:
- Laminar -- the separation point is a function of pressure gradient alone and as the pressure gradient becomes more adverse, the separation point moves further up the top surface of the body (provided it is adverse enough to induce separation to begin with). This happens independent of Reynolds number.
- Turbulent -- the separation point is a function of pressure gradient to leading order, with higher order influence from the Reynolds number. As the body speeds up, the pressure gradient becomes more adverse, and the separation point moves further up the top surface of the body (provided it is adverse enough to induce separation to begin with).
Looking only at varying Reynolds number is misleading because increasing speed for a fixed body in a fixed fluid varies more than just Reynolds number.
Looking at lift coefficients is misleading because lift can continue to increase even while increasing portions of the surface exhibit separation, until the separation is catastrophic (stall).