Some concepts do not understand about torque and angular momentum

Question

These are the knowledge points I got from online video.I finally found that there were some things I didn’t understand.

$\sum_n F_iR_i=\tau=I_{axis}a_z$,I learned from the previous video learning that the distance of R is the distance between each object and the axis of rotation.

BUT

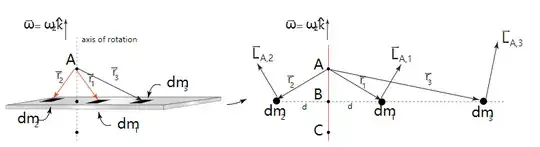
The next video is in the derivation of angular momentum about rotation.Before that, it is necessary to derive the angular momentum of a point $a$ and the object(This distance is the distance between the point $a$ and the object).

Because the total momentum (here is $mv$) is zero, This has nothing to do with the selection of points, which can be selected at will.So for simplicity, the rotation axis is selected.

$l=r_ap=mr_a^2w$;$I=mr_a^2=I_{axis}$;$l=I_{axis}w$

Why torque only considers the distance of the the axis of rotation and not the point, while the derivation of angular momentum needs to go from point to axis.

Answer 1

Torque on a particle is defined as $\vec r \times \vec F$ where $\vec r$ is the distance from the selected origin to the point where the force $\vec F$ is applied. The magnitude of the torque is $rFsin(\theta)$ where $\theta$ is the angle between $\vec r$ and $\vec F$. If we resolve the vector $\vec r$ into two components, one parallel to $\vec F$ and the other perpendicular to $\vec F$, the magnitude of the torque is $r_{perpendicular \enspace to \enspace F}F$; for rotation about a fixed axis this is the equation being used in your question above, summed over all particles (objects).

The direction of the torque is given by the right hand rule for $\vec r \times \vec F$.

Similarly angular momentum of a particle about a selected origin is $\vec r \times m \vec v$ where $m$ is mass and $\vec v$ is velocity; the magnitude of the angular momentum can be expressed as $r_{perpendicular \enspace to \enspace p} \vec p$, where $\vec p = m \vec v$ is the linear momentum, and $r_{perpendicular \enspace to \enspace p}$ is the component of $\vec r$ perpendicular to $\vec p$.

For a rigid body rotating about a fixed axis, the magnitude of torque is expressed as $I\alpha$ and the magnitude of the angular momentum is expressed as $I \omega$, where $I$ is the inertia of the body about the axis, and $\alpha$ and $\omega$ are the angular acceleration and the angular velocity, respectively, of each point in the body with respect to the axis.

See a good basic physics book, such as one by Halliday and Resnick.

(For general rotation of a rigid body about a point (not a fixed axis), the situation is complicated to evaluate and the inertia $I$ is a tensor. See a physics text on mechanics such as Mechanics by Symon or Classical Mechanics by Goldstein.)

Answer 2

Consider a thin mass-less rod, free to rotate around a friction-less perpendicular axle at one end. We will attach a point mass, m, to the rod at a distance, r, from the axle. Then (starting with the rod at rest) apply a force, F, perpendicular to the rod and axle at a distance, R, from the axle. The torque, acting over a (short) time, t, imparts an angular impulse to the rod and the rod transmits the torque and impulse to the mass: FRt = frt = (ma)rt = (mr)(at) = mrv = m$r^2$(v/r) = Iω. If other forces are applied, the torques add. If other masses are attached, the total torque is divided between them such that each has the same angular acceleration. Not that the big, R, is measured to the point of application of a force, and the little, r, is measured to the location of a mass. This logic can be extended to a solid object rotating about a fixed axle.

Answer 3

Both torque and angular momentum use the same moment arm calculation using 3D vectors.

$$ \vec{\rm torque} = \vec{r} \times \vec{\rm force} $$

$$ \vec{\rm ang.mom} = \vec{r} \times \vec{\rm momentum} $$

where $\times$ is the vector cross product, that disregards any parallel components of distance and only considers the perpendicular distance (called a moment arm). The vector $\vec{r}$ is measured from the origin.

The above is entirely analogous to the velocity of a point on a rotating body

$$ \vec{\rm vel} = - \vec{r} \times \vec{\omega} $$

And since you have $\vec{\rm momentum} = m\;\vec{\rm vel}$, the equation for angular momentum becomes

$$ \vec{\rm ang.mom} = \vec{r}\times ( m \, (-\vec{r}\times \vec{\omega})) = \underbrace{ -m\,\vec{r}\times \vec{r}\times }_{\rm mmoi} \vec{\omega} $$

Out of the equations above come all the planar projections that you are familiar with, like $F R = I \alpha$, or $I=m r_a^2$.