Griffiths, Introduction to Electrodynamics, prob. 5.59:
Prove that the average magnetic field over a sphere of radius R, due to steady currents inside the sphere, is $$ {\bf B}_{\rm ave} = {\mu_0 \over 4\pi} {2 \ \! {\bf m} \over R^3} $$ where ${\bf m}$ is the total magnetic dipole moment of the sphere.
This is the magnetic counterpart of this problem. My doubts arise right at the beginning. I'll use the symbol $ \overset {?}{=} $ to mark the equalities I haven't understood.
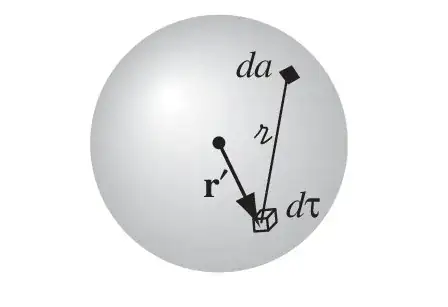
The centre of the sphere coincides with the origin of my frame of reference. $$ {\bf B}_{\rm ave} = {1 \over {4\over 3} \pi R^3} \int _{\tau} {\bf B}({\bf r}) \ \! d\tau = \\ {1 \over {4\over 3} \pi R^3} \int _{\tau} {\bf \nabla \! \times \! A}({\bf r}) \space d\tau \overset {?}{=} - {1 \over {4\over 3} \pi R^3} \oint _{\partial \tau} {\bf A}({\bf r})\! \times d{\bf a} = \\ - {1 \over {4\over 3} \pi R^3} \oint _{\partial \tau} \left[ {\mu_0 \over 4\pi} \int_{\tau}{{\bf J}({\bf r}')\over |{\bf r}-{\bf r}'| } d\tau ' \right] \! \times \! d{\bf a} \overset {?}{=} - {3 \mu_0 \over (4\pi)^2 R^3}\int _{\tau} {\bf J}({\bf r}') \! \times \! \left[\oint_{\partial \tau}{1\over |{\bf r}-{\bf r}'|} d{\bf a} \right] d\tau ' $$
The first $\overset{?}{=}$ seems to be Stokes' theorem, but sort of a generalized one. Is there a proof?
For the second $\overset {?}{=}$, the only explanation he gives is
Note that $\bf J$ depends on the source point $\bf r'$, not on the field point $\bf r$.