1

I know this is a very simple question, and I have searched it too. How to avoid incorrect symbols in calculation results.I don’t understand how to choose the sign of $ds$.

An object moves from a to b,Note the number $b<a$,$W>0$.

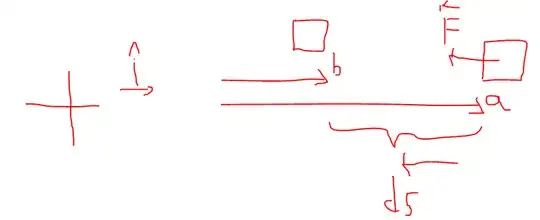enter image description here Take the direction of $i$ as the positive direction,Can I think of $\vec{ds}$ as $\vec{b}-\vec{a}$?

$\int _{a}^{b} {-F}{ds}=W<0$

I know that the choice of ab determines the positive and negative, maybe I should write $\int _{a}^{b} {-F}{ds}=w>0$

BUT 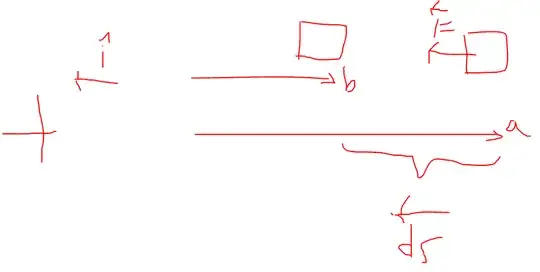enter image description here I changed the direction of i

Write the formula $\int _{a}^{b} {F}{ds}=W<0$

I can judge the positive or negative of the result by the order of the upper and lower limits of the integral and the sign of F. If it does not match, I will take the opposite sign for ds.I don’t want to judge and correct by the prediction result.

I can only modify the direction of ds through the results. It seems that this does not refer to the direction. Does it make sense to take positive and negative directions for ds?(I know that sometimes the direction is important,The positive and negative here refer to the positive and negative in the same direction)

How do I decide the sign of $ds$?Do I made any errors about the vector of ab and ds?

Eli
  • 13,829
能够可能
  • 35
  • 7

1 Answers1

1

First, you should pay attention to the integrand, which is the dot product of two vectors: $$\vec{F}\cdot\mathrm{d}\vec{r}.$$ You can't ignore that. Then you must pay attention to the coordinate system and state d$\vec{r}$ in coordinates appropriate to the problem. In Cartesian or rectangular coordinates $$\mathrm{d}\vec{r}=\hat{i}\mathrm{d}x + \hat{j}\mathrm{d}y + \hat{k}\mathrm{d}z.$$ Here is where many get tripped up. The differentials, like $\mathrm{d}x$, represent the positive coordinate changes and the limits of the definite integral define the actual path. So basically $\mathrm{d}\vec{r}$ tells us the positive direction change for our coordinate system and the integral limits tell us the actual path.

Applying this to your setup: a constant force of magnitude $F$ acts in the negative-$x$ direction on an object which moves from initial position $\vec{r}=(a,0,0)$ to final position $\vec{r}=(b,0,0)$. $$\vec{F}\cdot\mathrm{d}\vec{r} = (-\hat{i})F\cdot(\hat{i}\mathrm{d}x + \hat{j}\mathrm{d}y + \hat{k}\mathrm{d}z) = -F~\mathrm{d}x$$

Because the only integral is along an $x$-path and the limits are not functions of $y$ nor $z$, we only integrate in $x$. $$W = \int_a^b (-F)~\mathrm{d}x=-\left.Fx\right|^b_a = F\left(a-b\right)$$

So, if $b<a$, the work done by the force acting in the negative-$x$ direction is positive, which is proper. If $b>a$, the work is negative, again, proper.

Bill N
  • 15,522