I am currently studying Laser Systems Engineering by Keith Kasunic. Chapter 1.2.1 Temporal Coherence says the following:
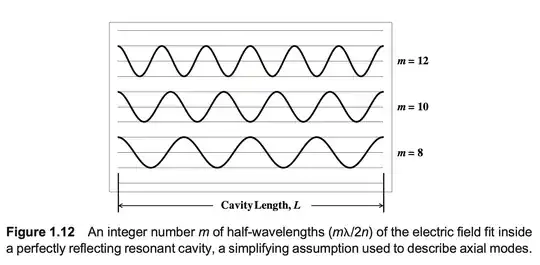
Axial (or longitudinal) modes are determined by the geometrical fit (or resonance) of a given wavelength in the laser cavity. That is, if the two mirrors that define a laser cavity are nearly planar and perfectly reflecting – an ideal assumption, given that one mirror will be designed not to be so that light can escape the cavity as output power – then Fig. 1.12 shows that an integer number $m = 1, 2, 3$, etc., of half-wavelengths of the electric field fit in the cavity length $L$: $$m \dfrac{\lambda}{2n} = L \ \ \ \ \ \text{[m]} \tag{1.4}$$ where the refractive index $n$ of the gain medium is included to account for the reduction in wavelength in comparison with its free-space ($n = 1$) value. With the exception of a specific type of semiconductor laser known as a vertical-cavity surface-emitting laser (VCSEL) with a cavity length $L \approx \lambda$, the number of half-wavelengths is large in practice. For example, for a HeNe laser emitting at $\lambda = 633$ nm with $L = 100$ mm and $n \approx 1$, $m = 2L/\lambda = 2 \times 0.1 \ \text{m} / 633 \ \text{nm} = 315,955$ half-wavelengths.
I understand the cavity length $m \dfrac{\lambda}{2n} = L$, as a standalone, but what is meant by "half-wavelengths" of the electric field, and how is this represented mathematically, in terms of electromagnetism and electromagnetic waves? And, relatedly, how does the $m$ values, as shown in figure 1.12, influence the electromagnetic waves themselves, beyond the simple equation of the cavity length $m \dfrac{\lambda}{2n} = L$ (that is, where in the mathematics of electromagnetic waves does the $m \dfrac{\lambda}{2n} = L$ come into play)?