Formula for centripetal acceleration: simple proof that does not use calculus?

Question

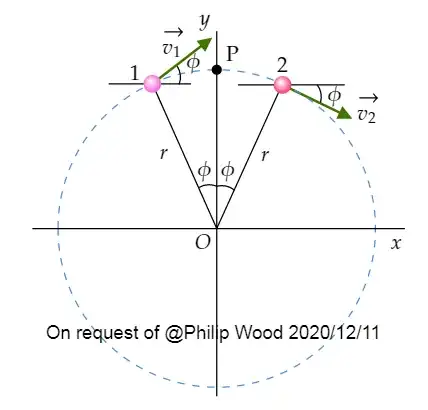
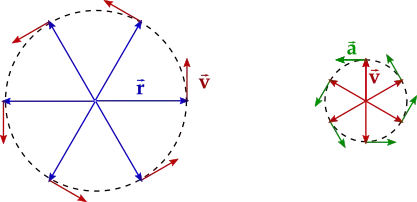
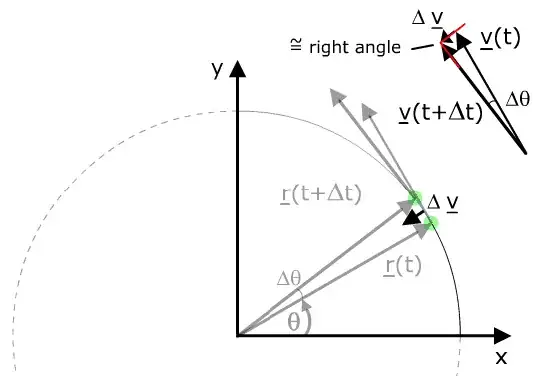
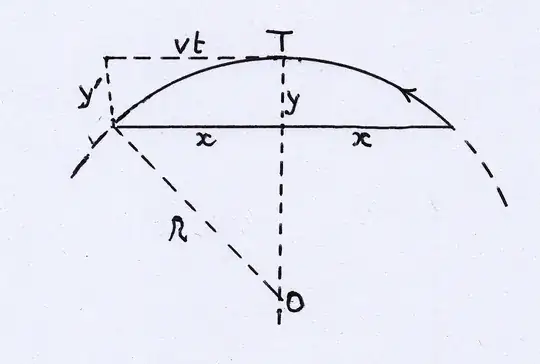
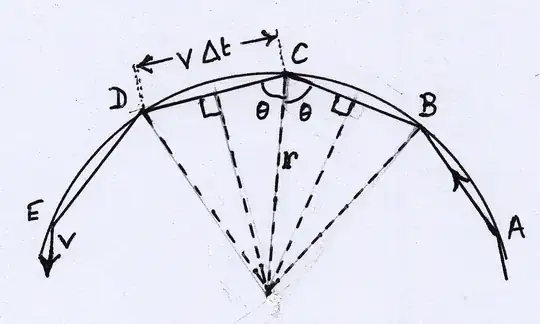
I teach physics to 16-year-old students who do not know calculus and the derivates. When I explain the formula for centripetal acceleration in circular uniform motion, I use this picture:

Here,

$$\vec{a}_{\text{av}}=\frac{\Delta \vec{v}}{\Delta t}=\frac{\vec{v}_2-\vec{v}_1}{\Delta t}$$

and

$$\vec{v}_1=(v\cos\phi){\bf \hat x}+(v\sin\phi){\bf \hat y}, \quad \vec{v}_2=(v\cos\phi){\bf \hat x}+(-v\sin\phi){\bf \hat y}.$$

Combining these equations gives

$$\vec{a}_{\text{av}}=\frac{\Delta \vec{v}}{\Delta t}=\frac{-2v\sin\phi}{\Delta t}{\bf \hat y}, \tag 1$$

which shows that the average acceleration is towards the center of the circle. Using $\Delta t=d/v=2r\phi/v$, where $d$ is the distance along the curve between points $1$ and $2$, gives

$$\vec{a}_{\text{av}}=-\frac{v^2}{r}\left(\frac{\sin \phi}{\phi}\right){\bf \hat y}.$$ As $\phi\to 0$, $\sin \phi/\phi\to 1$, so

$$\vec{a}_{\text{cp}}=-\frac{v^2}{r}{\bf \hat y}, \tag 2$$

which shows that the centripetal acceleration is towards the center of the circle.

Does there exist another simple proof of Equation $(2)$, in particular, that the centripetal acceleration is towards the center of the circle?

Answer 1

With no calculus, and for only uniform circular motion: consider the figure below.

On the left, we see the position vector $\vec{r}$ sweep out a circle of radius $r$, and the velocity vector $\vec{v}$ moving around with it. The tip of the position vector travels the circumference of the left-hand circle, which is $2 \pi r$, in one period $T$. Thus, $v = 2 \pi r / T$.

Now, acceleration is the rate of change of velocity, just as velocity is the rate of change of position. If we take all the velocity vectors from the left-hand diagram and re-draw them at a common origin, we see that the velocity vector must also sweep out a circle of radius $v$. The tip of the velocity vector travels the circumference of the right-hand circle, which is $2 \pi v$, in one period $T$. The acceleration vector, being "the velocity of the velocity", must by analogy have magnitude $a = 2 \pi v / T$. Thus, $$ \frac{a}{v} = \frac{2 \pi}{T} = \frac{v}{r} \quad \Rightarrow \quad a = \frac{v^2}{R}. $$ We can also see from the diagram that at any time, $\vec{a}$ is directly opposite the direction of $\vec{r}$, i.e., directly towards the center of the circle.

Credit goes to my Grade 11 physics teacher, Mr. Imhoff, who showed me this trick over 20 years ago.

Answer 2

Let's consider a small time slice $\Delta t$ of the circular motion.

_{(image from PhysClips - Circular motion)}

The position vector rotates by an angle $\Delta\theta$, thus changing from $\vec{r}(t)$ to $\vec{r}(t+\Delta t)=\vec{r}(t)+\Delta\vec{r}$.
When the angle $\Delta\theta$ is small, then $\Delta\vec{r}$ is nearly perpendicular to $\vec{r}$. Then we have $$\Delta\theta=\frac{|\Delta\vec{r}|}{r} \tag{1}$$

Likewise the velocity vector rotates by the same angle $\Delta\theta$, thus changing from $\vec{v}(t)$ to $\vec{v}(t+\Delta t)=\vec{v}(t)+\Delta\vec{v}$.
Again, when the angle $\Delta\theta$ is small, then $\Delta\vec{v}$ is nearly perpendicular to $\vec{v}$. Then we have $$\Delta\theta=\frac{|\Delta\vec{v}|}{v} \tag{2}$$

By equating (1) and (2) we get $$\frac{|\Delta\vec{v}|}{v} = \frac{|\Delta\vec{r}|}{r} \tag{3}$$

By the definition of acceleration we have $\Delta\vec{v}=\vec{a}\ \Delta t$, and by the definition of velocity we have $\Delta\vec{r}=\vec{v}\ \Delta t$. When we insert these into (3) we get $$\frac{|\vec{a}\ \Delta t|}{v} = \frac{|\vec{v}\ \Delta t|}{r}. \tag{4}$$

Here we can cancel $\Delta t$, write $a$ for $|\vec{a}|$, and $v$ for $|\vec{v}|$. $$\frac{a}{v} = \frac{v}{r}$$

Finally we bring $v$ from the left to the right side and get $$a = \frac{v^2}{r}$$ which is formula of the centripetal acceleration.

Answer 3

Yes!

The position of particle moving in circle can be written as:

$$ \vec{r(t)} =R \left[ \cos( \theta) \vec{i} + \sin( \theta) \vec{j} \right] \tag{1}$$

Differentiate,

$$ \vec{v(t) } = \omega R\left[ \cos(\theta) \vec{j} - \sin(\theta) \vec{i} \right] \tag{2}$$ Where $$ \frac{ d \theta}{dt} = \omega$. Differentiating again,

$$ \vec{a(t)} = - \omega^2 R \vec{r(t) } \tag{3}$$

Take the magnitude of equations (1),(2) and (3):

$$| \vec{r(t)} |= R \tag{1'}$$ $$ |\vec{v(t)} | = R \omega \tag{2'}$$ $$ |\vec{a(t) } |= R \omega^2 \tag{3'}$$

Simplfying,

$$ |\vec{a(t)} | = \frac{ | \vec{v^2}|}{|\vec{r}|}$$

Answer 4

There is a way to arrive at the magnitude of the centripetal acceleration that takes full advantage of various symmetries of the setup.

In cases where the velocity is constant we have the following oppertunity to simplify: instead of using differential expressions we can use sizable lengths of distance with sizable durations.

In the case of circular motion the magnitude of the velocity is constant, and the direction changes at a constant rate.

Under those special conditions it is sufficient to express velocity as follows:

$$ v = \frac{\Delta r}{\Delta t} \qquad (1) $$

In the above expression $\Delta r$ stands for 'the accumulated change of position'.
(I'm adding the word 'accumulated' because after a complete revolution there is of course no net change of position. But what matters is that there is a process of continous change of postion.)

I will used the capital letter 'T' for the duration of a complete revolution.

Over the duration of a complete revolution the distance traveled is $2\pi r$

Therefore:

$$ v = \frac{2 \pi r}{T} \qquad (2) $$

The next step capitalizes on the following abstract symmetry:

Velocity is the time derivative of position.
Acceleration is the time derivative of velocity.

That is a repeated pattern. It's one level up, but the pattern is identical

The magnitude of the acceleration is constant, and the direction changes at a constant rate. Therefore using infintisimals isn't necessary, the following is sufficient:

$$ a = \frac{\Delta v}{\Delta t} \qquad (3)$$

Over the duration of a complete revolution the accumulated change of the velocity vector follows the same pattern as the accumulated change of position vector.

Therefore:

$$ a = \frac{2 \pi v}{T} \qquad (4) $$

Using (2) to eliminate 'T' from (4);

$$ a = 2 \pi v \frac{v}{2\pi r} \qquad (5) $$

$$ a = \frac{v^2}{r} \qquad (6) $$

Just to be clear: I recognize of course that this will be a hard sell to high school students. Thinking of the set of all velocities as a geometric space is quite an abstraction.

I imagine an animation could do a lot here. This animation would first show revolution of the postion vector, and then the animation takes the origin of the velocity vector as a stationary point, and then shows a revolution of the velocity vector.

Answer 5

Here's an attempt.

First for the magnitude $|\vec{a}|$: use dimensional analysis. For uniform circular motion the only independent quantities are $|\vec{v}|,m,r$. Therefore we must have $|\vec{a}|=C |\vec{v}|^2/r$ for some constant $C$.

For the direction of the acceleration vector: you can take $\vec{a}$ and project to its parallel component along $\vec{v}$ and its component perpendicular to $\vec{v}$. The parallel component will increase/decrease $|\vec{v}|$, if the parallel component is nonzero. However, for uniform circular motion, this cannot be the case. Therefore, $\vec{a}$ is perpendicular to $\vec{v}$.

Then there are two alternatives: either it always points towards the circle centre, or it always points away from the circle centre. I believe the students should intuitively understand that the last possibility is ridiculous. So now they understand uniform circular motion, notwithstanding the constant number $C$ which you cannot determine from this argument.

Answer 6

I think this is easy to understand:

with $~\Delta v=v\,\Delta\varphi$

$$a=\frac{\Delta v}{\Delta t}=v\,\frac{\Delta\varphi}{\Delta t}=v\,\omega$$

and $$ v=\frac{\Delta s}{\Delta t}= \frac{R\,\Delta\varphi}{\Delta t}=R\,\omega$$ where $~\frac{\Delta\varphi}{\Delta t}=\omega=~$constant and $\Delta s~$ is the line element on the circle.

thus :

$$a=R\,\omega^2=\frac{v^2}{R}$$

Answer 7

A very simple derivation that requires no calculus is the following. We use the fact that there is a perfect mathematical analogy in which the velocity vector is to the radius vector as the acceleration is to the velocity. Writing $r$, $v$, and $a$ for the magnitudes, the analogy allows us to infer that if $v=2\pi r/T$, then $a=2\pi v/T$. Eliminating $T$ then gives $a=v^2/r$.

Answer 8

This derivation is based on one of c1659 by Christiaan Huygens. I include it for interest rather than because I think it the best way to teach centripetal acceleration to high school students!

Suppose a particle is whirled in a circle on a thread. At time $t=0$ the particle is at point T, the thread breaks and the particle carries on in a straight line at speed $v$.

At time $t$ the particle has travelled $vt$ from T. It is now a distance $y'$ from the point on the circle where it would have been if the thread hadn't broken.

If $t$ is small, then $\ \ \ \ \ \ \ vt \approx x$

and $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y' \approx y$

But using Pythagoras's theorem (or the intersecting chords theorem) we can show that for $y<<r$, $$x^2 \approx 2ry$$ As $t$ approaches zero, all these approximations become exact, so $$y' = \frac12 \frac{v^2}{r} t^2$$ But the displacement of a particle starting from rest and experiencing an acceleration $a$ is given by $$s= \frac12 a\ t^2$$ We see then, that our particle's acceleration, had the thread not broken, would have magnitude $v^2/r$ and (remembering that $t$ is approaching zero) would be directed towards the centre of the circle!

Answer 9

Your students might like this approach. It uses Newton's technique of modelling a smooth change as a series of sharp, sudden changes.

Consider a particle bouncing around the inside of a cylinder, following a path that is a regular polygon.

The change of velocity at each bounce, for example at C, is clearly $$\Delta v=2v\ \cos \theta\ \ \ \text{towards the circle centre}$$ The time, $\Delta t$, between bounces is $$\Delta t = \frac{\text{CD}}{v}=\frac{2r\ \cos \theta}{v}$$

If we make the side length of the polygon smaller and smaller (by making $\theta$ approach $\pi /2$) then any small arc contains a large number $n$ of bounces and the same number of intervals $\Delta t$, so the mean rate of change of velocity is $$a=\frac{n\Delta v}{n\Delta t}=\frac{v^2}{r}.$$ In the limit the polygon approaches a circle, and the mean acceleration becomes the instantaneous acceleration.

This method is essentially a variation on the classic derivation in the question. It avoids explicit use of $\lim \limits_ {\theta \to 0} \frac{\sin \theta}{\theta}=1$. Instead, the taking of this limit is hidden in the demand to consider smaller and smaller lengths of side of the polygon, so the polygon becomes a circle.

Answer 10

You should be careful about using the concept of limits for students that haven't taken calculus. Without that background, any derivation based on limits comes down to hand waving, and getting students used to relying on hand waving is dangerous. It encourages them to engage in hand waving themselves, and discourages them from developing the proper conceptual understanding when they later learn the framework in which to have that understanding.

If this is a physics class, then you can use physics concepts to motivate these results. but you should keep in mind that without the math background, this is motivation, not proof.

If this is uniform circular motion, then by symmetry the speed (absolute value of velocity) and kinetic energy are constant. This means that the centripetal force is doing no work, hence it must at all times be perpendicular to the velocity.

As far as the magnitude of the acceleration, it is probably easier to explain in terms of $\omega$ rather than $v$: the magnitude of the velocity is $\omega r$, and its direction is rotating at the rate of $\omega$, hence it is changing at a rate of $\omega^2r$. I would not pretend for this to be a rigorous proof; I would tell my students "Here's something that helps explain where this formula come from. When you get to calculus, you'll be able to rigorously prove it."