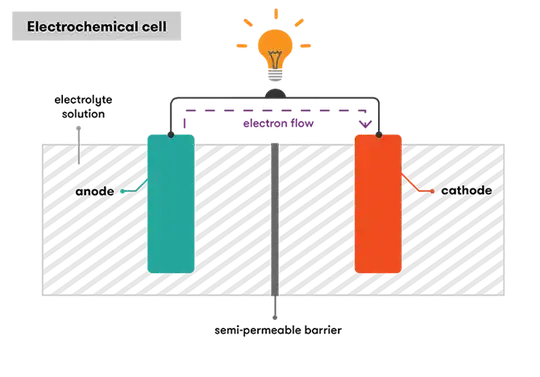
The explanations that I've seen for how batteries work (like this one) tend to go along these lines:
One electrode "has an electrochemical potential that makes it want to give up electrons" (or really, ionize neutral atoms) and the other "has an electrochemical potential that makes it want to accept electrons" (or really, recombine electrons and ions into neutral atoms). The electrolyte solution that connects the two electrodes allows positive ions to pass through, but not electrons. Before an external circuit is closed, positive ions leave the negative electrode and move through the electrolyte solution onto the positive electrode, leaving both electrodes with a slight net electric charge. These net charges produce an electrostatic field within the battery from the positive to the negative electrode that tends to oppose the motion of ions through the electrolyte solution. This electrostatic field builds up until it cancels the electrochemical potential and the battery reaches an equilibrium.
Once an external circuit is closed, the electrostatic field passing through the wire draws electrons from the negative electrode to the positive electode, slightly reducing the charge imbalance and weakening the internal electric field within the battery. This allows the positive ions to resume flowing through the electrolyte solution, which restores the charge imbalance and the potential difference, which in turn continues to draw electrons through the wire, etc.
To me, this explanation seems to be invoking the "electrochemical potential" as a magic wand that pushes positive ions from the negative to the positive electrode without needing to invoke any electric fields. I'm okay with that for the most part; it's obviously useful to use bulk thermodynamic potentials to simplify the immensely complicated behavior of a many-body system. I'm also okay with treating the electrolyte solution as a black box that magically allows positive ions through while blocking free electrons.
But the thing that I really don't understand about this explanation is the fact that within the electrolyte solution, the electric field always points from the positive to the negative electrode - but when the circuit is closed, the positive ions, and hence the net current, flow from the negative to the positive electrode (because the electrochemical potential "beats" the slightly weakened electric field). This means that the electrical conductivity of the electrolyte solution is actually negative, because the electric field and current point in opposite directions!
This is just very weird to me. At the microscopic level, charges just move in whatever direction the electric field pushes them. (I'm assuming that batteries can be qualitatively explained without invoking either magnetic or quantum effects, although maybe that's not true.) How can this magical stat-mech "electrochemical potential" overcome the basic rules of electrostatics and cause charged ions to move against the electrostatic field, resulting in an electrolyte solution with a negative electrical conductivity? I don't have any intuition for what's going on here at the microscopic level, or for how the positive ions could move through the electrolyte solution in this way. To me, this explanation simply shifts the question from "How do batteries work?" to "How does the electrochemical potential work?".
ETA: I found a paper that addresses exactly this question.