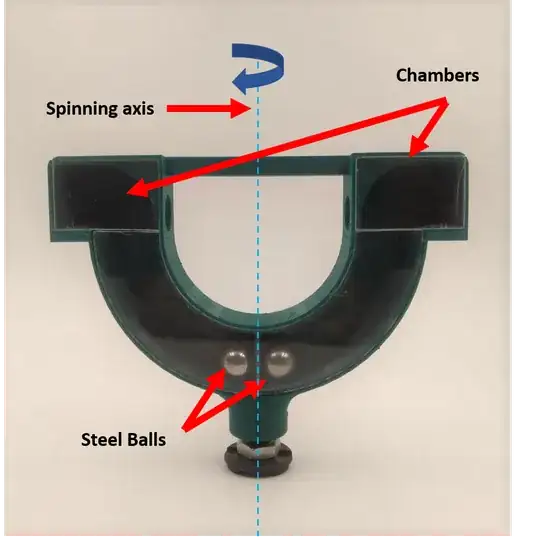
I made a classical experiment to demonstrate centrifugal force. The experimental setup is made to stand vertically and spun along the vertical axis. The balls that initially rest at the bottom, on spinning, move up to the chamber. Can someone please explain in layman terms as to why this happens? I have added images. Free body diagrams can be of great help.
10 Answers
When spun around the balls are set in motion. That motion would continue in a straight line if it wasn't for the wall. The wall causes the motion (the velocity) of each ball to turn all the time. (This is where the centrifugal effect comes from - the balls "feel" swung outwards because they want to continue in a straight line but the wall is in the way.)
It does so with a normal force. But since the wall is tilted at the lower part that normal force is tilted as well (it is always perpendicular to the wall). Meaning that the normal force has not just a horizontal component which causes the turning as described above, but also a vertical component.
It is this vertical component that causes the ball to rise up.
- 53,191
I made a classical experiment to demonstrate centrifugal force.
Just to clarify, It's only centrifugal in a rotating frame and centripetal in an inertial one. Confusing?Here is a good distinction between the two.
As per your current understanding, Il explain it to you in the frame of the rotating stand. Picture it as the stand being still and the entire earth rotating instead.
In this frame, the ball would feel something pushing it outwards this is the centrifugal force. Again it's only centrifugal in this frame. Not in the frame of an observer.
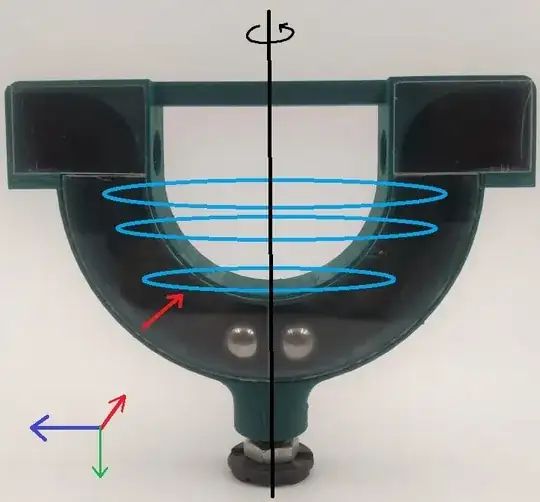
At every instant in the ground frame, the ball spins around an instantaneous circle which I colored light blue in the attached picture, It is due to this rotation a centrifugal force acts in the first place.
(Dark blue vector: centrifugal force, Red vector: normal force, Green vector: gravity)
A normal force also acts it will not be in the same direction as the centrifugal force. This force will help push it up and also cancel a little bit of the centrifugal force, As you can see in the little diagram in the bottom left corner.
It is the resultant of the vertical component of the normal force and gravity that contribute to the rise of the ball and it is the resultant of the centrifugal force and the horizontal component of the normal force which contribute to the radially outward swing of the ball.
- 2,133
- 1
- 12
- 29
The question asks for an explanation "in layman terms", so I will try to provide one.
The term "centrifugal force" is problematic. But the other answers have covered this already, so I won't. In fact, I won't mention forces at all.
Imagine you suddenly remove the curved stand while the balls are moving. The balls will move away from the axis. Not directly away, but for the purpose of this experiment, we can pretend that they are moving directly away from the axis.
Now let's look at a simpler, but for our purposes, equivalent situation. Imagine a ball rolls across a flat surface, before hitting a section that slopes upwards (and is strong enough that the ball can't just bend it or go through it). When the ball hits this section, it will move up. Why? There are only two other possible outcomes:
- The ball goes through the surface.
- The ball instantly stops moving horizontally.
Clearly, these are both absurd.
- 446
- 2
- 8
you have two external forces that act on the ball , the centrifugal force ,$~m\,\omega^2\,y~$ and the weight force,$~m\,g~$
the ball move towards the instantaneous tangent on the curve due to the resulting force (centrifugal force plus weight force) towards the tangent , but only if the resulting force greater then zero.
Remark:
the normal force is constraint force that perpendicular to the instantaneous tangent vector and not affected the ball motion.
- 13,829
It is easier to understand if we compare with the situation of the balls in a plane rotating disk as described in this question.
In that case, the balls would increase continuously its velocity, while migrating to points with higher disk tangential velocities.
In the present case, instead of a continuous increase of the kinetic energy, part of it becomes potential energy, with the balls climbing. If the angular velocity is high enough, they reach the chambers.
- 17,607
What you see here is inertia
The balls don't like to change their direction. They like going in straight lines. Now, if they were at the bottom, they'd have a much tighter curve. It is like when driving. A tighter curve feels a lot "heavier" than a gentle curve.
So the balls do a tradeoff. They accept a higher speed (kinetic energy!) and a higher gravitational potential (they go upwards) in order to get a gentler ride (less tight curve)
It all checks out matematically too. The universe does its calculation and the balls are literally dragged out to the side and up top. Just like the experience you have, when driving through a tight curve. You also feel the universe dragging you out to the side. Fortunately, in most cases, the car has good enough tires to withstand the urge to slide off the road.
- 324
The ball rises so that the constraining force of the chamber on the ball can provide a centripetal force to keep the ball rotating with the chamber. (There is no centrifugal force in the inertial frame.) For a frictionless, circular chamber you can calculate the position up the chamber that the ball rises using a simple force balance in the inertial frame. Solution follows for the steady state. Note that the faster the rotation of the chamber the farther up the ball rises. (You can also do the evaluation in the rotating non-inertial frame considering the centrifugal force present in that frame.)
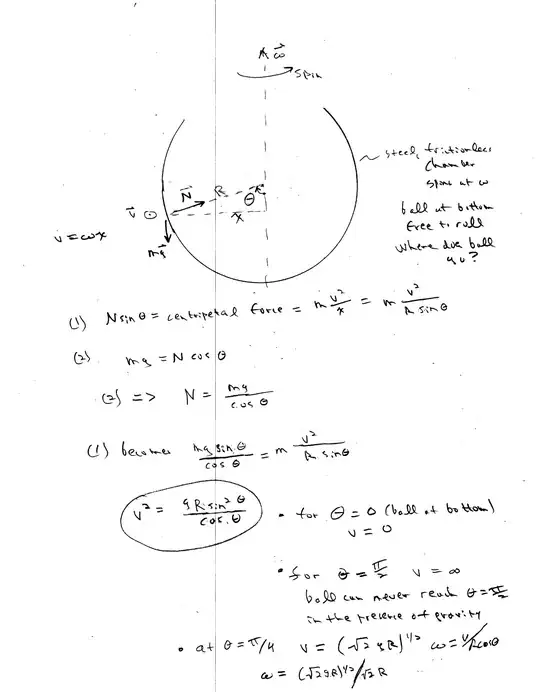
- 16,825
- 2
- 45
- 73
- 9,601
I am going to try to answer with one sentence.
The balls want to move as far away from the rotation axis, and the "up" position gives them an opportunity to do so for the given shape of the grooves.
- 40,139
I use the classic ice-skater style analogies (modified).
Imagine spinning yourself and holding your partner out at arms length spinning around you.
Lets assume a light partner to make it easier for this exercise.
If you let go of them they will fly off away from you.
The balls are doing the same, you are spinning around them around a center and with no 'arms' to hold them they heads outwards from the spin (gravity to small to be active here) and in this case that means away and then up the slopes to the chambers.
Of course what's interesting is that how much they do that (climb the walls) is dependent on the speed of the spin. and probably weight of balls, height of walls, etc.
I like it when we let the balls climb the walls but then again I like rhyming stuff too for you.
- 319
Sorry, no diagram, but I still hope this will be helpful. As people have pointed out, this is maybe not a full answer, so you can regard this as hints for a fun exercise.
The terminology "centrifugal force" never makes sense, to me, and only causes confusion. We should throw out the whole idea of "centrifugal force", and use only centripetal acceleration (NOT force!), combined with Newton's Second Law.
If a particle moves in a circle at constant speed, its acceleration (not force!) is directed towards the centre of the circle, by differentiating the position vector twice with respect to time.
So, if you assume that a particle is moving in a circle (at constant speed), then this tells us the acceleration. (By the way, if the speed is varying also, then the acceleration is almost always NOT towards the centre! EDIT: yes, I really do mean "almost" here, because the acceleration vector can instantaneously point towards the centre in some cases. You can see this by differentiating exp(if) for a general real-valued function f.)
Therefore, by Newton's Second Law, the RESULTANT force on the particle must also be towards the centre of the circle. Note that there are only TWO forces acting on the ball: gravity (pointing down) and the normal (reaction) force (pointing perpendicularly away from the surface pushing against the balls). THERE IS NO CENTRIFUGAL FORCE!
EDIT: if you disagree, then it's really just semantics about what "force" means. There is no actual physical force pushing outwards. The fact that you "feel" a force doesn't make you correct; it just demonstrates that some physical measurements do not give complete information about the system in question. See Does centrifugal force exist?
If you know the acceleration, then Newton's Second Law does NOT tell us all the different individual physical forces acting on the particle; it only tells us the RESULTANT force.
For example, if you spin a ball around on the end of a rope, then the physical forces are different in nature to this example, even though the acceleration is the same. You could also have magnetic fields etc. etc., but there would be no way to tell simply from the motion of the ball what forces are acting.
For a complete answer as to why the balls move upwards as you increase the rotation frequency, you have to write down the equations for the normal force, depending on the height of the balls. Assume first that the balls are instantaneously at exactly the correct rotation speed to remain at a fixed height, and consider what happens if the speed is changed by a small amount (i.e., a small perturbation from a system at equilibrium).
Since normal force is limited by the component of the ball's gravity pressing against the surface, it's not possible for the vertical component of the normal force to counteract the gravitational force fully if the rotation is too slow, so the ball must move downward.
In the other direction, if the rotation is too fast, the horizontal component of the normal force (to provide the centripetal acceleration) must be so great that the upwards vertical component of the normal force is greater than gravity, so the ball will tend to move upwards.
Of course we are neglecting friction and air resistance, and possible rotation of the balls themselves in addition to the circular motion (i.e., the ball is not a particle).
For a really good answer (even for a particle without friction/air resistance), you'd have to write down an equation for the rotational frequency, as a function of time, and solve some differential equations for the motion of the ball, but probably you don't want to do this. But strictly speaking, I don't think there's any simpler way to solve it properly - no amount of diagrams and geometry will give you the full answer without calculus.
EDIT: to be clear: any complete, quantitative answer MUST allow the rotation speed to vary, and so the usual calculation of centripetal acceleration for constant speed above does NOT apply. This is why I say that you cannot possibly understand this properly without at least the concept of differential equations with vector variables. However, if you DO know about these mathematical topics, and Newton's Second Law, then no other knowledge is required to solve this - but it's not particularly easy. It's a bit like trying to understand constant acceleration linear motion without calculus: even though it's a very special case of the general equations, there is simply NO correct way to understand it properly without calculus [or something mathematically equivalent in the special case], so if you're serious then you just have to learn it.