In the collision between the red disk (mass $m_1$) and the green disk (mass $m_2$) as shown bellow, why the force that mass 1 makes on mass 2, $\mathbf{F}_{12}$, is along the line connecting the point of contact and the center of the ball (green arrow)?
Is this always true? Is there a simple explanation for this?
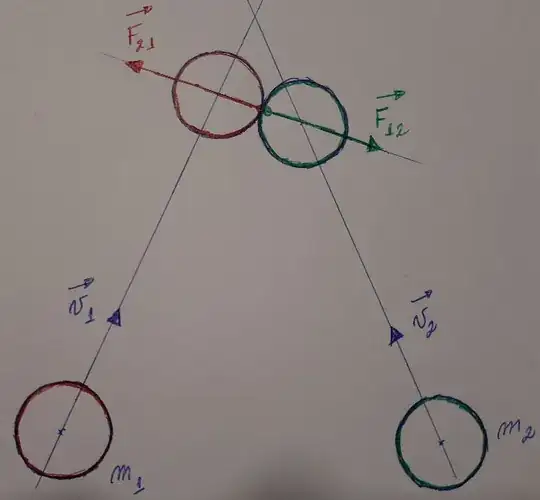
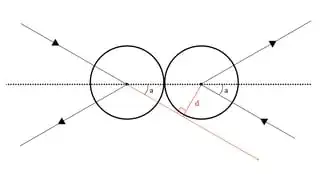
Why? Because that is the only direction where relative motion is not allowed. The centers cannot get any closer to each other.
If force was along a direction where motion was allowed, then the contact force would do work and either add or remove energy to the system violating the conservation of energy. The only time the contact force is at an angle to the contact normal is when friction is involved.
This rule can be generalized as follows
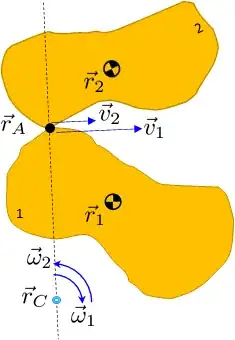
The line of action of the contact force must pass through the instant center of rotation between the two bodies.
At the instant center, the two bodies have zero relative velocity (only relative rotation) and thus the power transmitted through the contact is also zero.
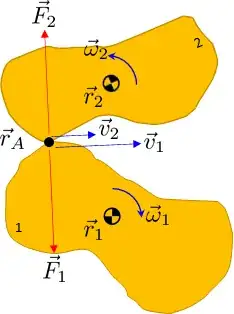
The direction of the contact force is always such that
$$ \vec{F}_1 \cdot (\vec{v}_1 - \vec{v}_2) = \vec{F}_2 \cdot (\vec{v}_2 - \vec{v}_1) = 0 $$
when you work out the relative instance center of rotation (point C below), it will always fall on the line along the contact normal.
It means that there is no friction between the disks. Otherwise the forces would not be in the same line, and the resulting torque would cause a rotation of the disks after the collision.
In an idealised case: yes. You can decompose the force that is acting at the boundary in two parts: the normal force and the tangential force. The normal forces prevents objects from moving through eachother so this always appears when you try to move to objects into one another. The tangential force often occurs as a result of friction when two surfaces move with respect to eachother. You are probably familiar with this picture for the more simple case of the normal force:
It is easiest to reason from the center of mass frame. If the collision is head-on (the paths and velocities are parallel) then it is easy to see the tangential force is zero. So the force is normal to the surface so it is along the line connecting the point of contact and center of mass.
When the collision is off-centre, like in the picture below, it gets more complicated. When we assume friction is zero the tangential force is still zero. This is still an approximation since in real life the normal force is a result from the balls deforming and this doesn't happen instanteneously. But we only care about the ideal balls for now. When friction isn't zero we can have a tangential force. In the picture the left ball and right ball are moving in opposite directions so the surfaces have some relative velocity. If there is friction the balls get a nonzero torque which makes the ball spin and it can change the direction in which they leave the collision.
source of the first picture: Why is normal force perpendicular?
