I often read from textbooks that in relativity, space and time are treated on an equal footing. What do authors mean when they say this?
Are there any examples that show space and time are treated on an equal footing? Conversely, what examples show that space and time are not treated on an equal footing?
After some thought, this is what I understand:
In Newtonian physics, a particle's path can be specified by $x^i(t)$ where the time $t$ can be seen as an independent parameter. The space coordinates $x^i(t)$ are dependent variables that depend on $t$. We thus say that space and time are not treated on an equal footing.
In relativity, a particle's worldline is specified by $x^\mu(\lambda)$ where $\lambda$ is an independent parameter (often taken as the particle's proper time). Both space and time coordinates $x^\mu(t)$ are dependent variables that depend on $\lambda$. We thus say space and time are treated on an equal footing.
Putting space and time on the same footing means to treat time as another dimension in addition to the other three physical dimensions. In the context of relativity, time is treated as another dimension (but within this idea of Spacetime space and time are not the same).
In classical Newtonian physics, space is treated within the ideas of three dimensional space. In this approach, time is absolute, as oppose to relativity.
I often read from textbooks that in relativity, space and time are treated on an equal footing. What do authors mean when they say this?
I actually give a brilliant aid to understand what does it mean? It's called surveyors parable introduced by Tayloe and Wheeler. Suppose a town has daytime surveyors, who have the North star. These notions differ, of course, since the magnetic north is not the direction to the North pole. Suppose, further that both groups measure north/south distances in miles and east/west distances in meters, with both being measured from the town center. How does one go about comparing the measurements of the two groups?
With our knowledge of Euclidean geometry, we see how to do this: convert miles to meters (or vice versa). Distances computed with the Pythagorean theorem do not depend on which group does the surveying. Finally, it is easily seen that the 'daytime' coordinate can be obtained from the 'nighttime' coordinate by a simple rotation. The geometry of this situation is therefore described, in which the $x$ and $y$ directions correspond to geographic east and north, respectively, and the $x'$ and $y'$ directions correspond to the magnetic east and north, respectively. If the surveyors measure $x$ and $x'$ in meters, and $y$ and $y'$ in miles, and if they do not understand how to convert between the two, communication between the two groups will not be easy.
Applying the lesson of special relativity, we should measure both time and space in the same units. How do we measure distance in second? That's easy: simply multiply by $c$. This has the effect of setting $c=1$ since the number of seconds traveled by light in 1 sec is precisely 1.
Are there any examples that show space and time are treated on an equal footing? Conversely, what examples show that space and time are not treated on an equal footing?
In Newtonian mechanics, We never care about time, it's flowing at a constant speed. At the same rate for all the observers in the universe.
While If you look at special relativity you always find that time is one of the coordinates just like the other 3 coordinates are. Like the following
According to Newtonian mechanics, If a rod is moving with some speed, all observers in the inertial frame will agree on the length of the rod. But If you work out the space-time diagram for the moving rod. It will look like :
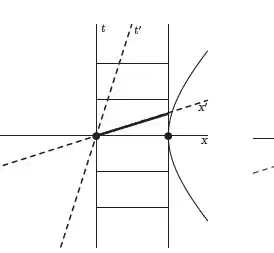
As you can see for the moving observer the length of the rod gets contracted. (It needs some elementary knowledge to appreciate it). Drawing the same for Newtonian nothing will change. As time and space, axis remains parallel to rest obersevers frame.
In Special Relativity, there is the invariant interval defined as $$\Delta s^2=c^2\Delta t^2-\Delta x^2$$ (for relative motion in the x-direction only). Here $\Delta t$ and $\Delta x$ are the difference in t and x for two events in some frame of reference. It has the same value in any other inertial reference frame using that frame's coordinates t' and x' to describe the same two events.
As t and x both appear in the equation in a similar fashion, one might say that time and space are being treated on an equal footing.
