A tilted disk rolling on the floor

Question

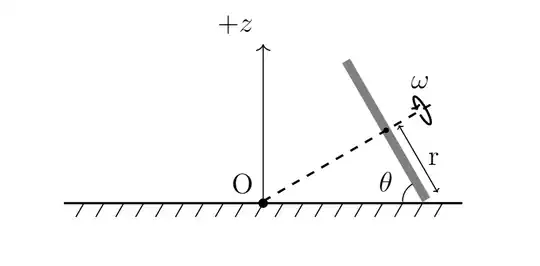
First of all, an image to describe the situation we have:

Background

A uniform disc is rolling without slipping on a flat surface. The disc itself is also in circular motion about the point $O$. I have tried this with a roll of cellotape so the situation itself seems plausible. What I want to find is the radius of the disk in terms of $g$, $\omega$ and $\theta$.

My analysis

(apologies for the lack of any diagrams from here onwards)

Now, something must be keeping the disc from just falling over. If I take the angular momentum about the point of contact, I get $\overrightarrow{L}=\frac{3}{2}mr^2 \omega$. The vector itself is angled at $\frac{\pi}{2} - \theta$ to the floor, and is swinging around as the disk moves in space.

Some force is providing the torque for this to be possible. This force is the gravitational acceleration. There is no torque due to normal, frictional or centrifugal forces (?) about the point of contact. If we compute the torque due to gravity about the point of contact, we get $\overrightarrow{\tau} = mgr \cos{\theta}$.

The angular momentum vector is rotating about an axis perpendicular to it and inclined at $\frac{\pi}{2} - \theta$ to $+z$. Let us call the angular velocity about this axis $\Omega$. We can find $\Omega$ by picking the center of mass of the disc to study. The distance from $O$ to the COM is $r\tan{\theta}$. So we have $\Omega r\tan{\theta} = \omega r$, therefore $\Omega = \omega \cot{\theta}$.

Therefore, we can find the required torque to be $\overrightarrow{\tau}_{req} = L \Omega$. Equating $\overrightarrow{\tau}_{req}$ and $\overrightarrow{\tau}$, we get $$r = \frac{2g \sin{\theta}}{3 \omega^2}$$

Can someone please check my analysis? Since I came up with this myself, I don't have anything to refer to. (I also feel a little unsure whether centrifugal force has any role here.)

Answer 1

This problem is in Introduction to Classical Mechanics by David Morin as problem 9.23.

Let the rate of precession of the coin be $\Omega$. Let the moments of inertia be $I = \frac 14 mr^2 $ and $I_3 = \frac 12 mr^2$ respectively. In this situation, it is most convenient to find $\mathbf{L}$ about the center of the coin.

The important thing here is to (temporarily) forget about the motion of the center of the coin in space (as it does not contribute to the changing part of $\mathbf L$). The angular velocity is then $\mathbf{ω}-\Omega \hat{\mathbf{z}}$. The minus sign occurs because they point in opposite directions.

Your mistake is that you failed to include the $-\Omega\hat{\mathbf{z}}$ part of the coin's rotation. The coin, on top of spinning about $I_3$ with angular velocity $\omega$, is also rotating about the $z$-axis with angular velocity $\Omega$. This can be most easily visualized by imagining yourself sitting some height above the center of the coin, always facing in the direction of the $x$-axis.

The next few lines is the heart of the problem.

Now, we are interested in finding the non-vertical component of $\mathbf{L}$, which we shall denote as $L_{\parallel}$. The $\mathbf{ω}-\Omega \hat{\mathbf{z}}$ can be reexpressed as $\omega - \Omega \cos\theta$ perpendicular to the coin and $\Omega \sin\theta$ downwards along the coin.

$\omega - \Omega \cos\theta$ perpendicular to the coin translates into a contribution $I_3(\omega - \Omega \cos\theta)\sin\theta$ to $L_{\parallel}$.

$\Omega \sin\theta$ downwards along the coin translates into a contribution $I\Omega \sin\theta \cos\theta$ to $L_{\parallel}$.

Putting the above two together gives us a total of $$L_{\parallel} = mr^2 \left(\frac 12 \omega \sin\theta -\frac 14 \Omega \sin\theta \cos\theta\right)$$ Since $L_{\parallel}$ is precessing with frequency $\Omega$, we must also have $$\left| \frac{\text d \mathbf{L}}{\text dt}\right| = L_{\parallel} \Omega$$

The other equations are $$R \Omega = r\omega$$ $$F_f = m(R-r \cos\theta)\Omega^2$$ $$\left| \frac{\text d \mathbf{L}}{\text dt}\right|= r(mg\cos\theta - F_f \sin\theta)$$ where $R$ is the radius of the point of contact and $F_f$ is the friction. Solving all the equations will obtain $$\Omega = \sqrt{\frac{g}{\tan\theta \left( \frac 32 R - \frac 54 r \cos\theta\right)} }$$ Therefore, precession is only possible when $R > \frac 56 r \cos\theta$.