5

This question is inspired by another one about the simplest model of topological insulator, where 4tnemele showed a nice two band model in the answer.

I read that and am wondering if we and push that to one dimension.

For example, by analogy to the graphene case, if we have a Hamiltonian in 1D (say x) as $H(k_x)=(k_x-k_0)+m$ for $k_x>0$. When $k_x=k_0$, one has $m>0$. $H(k_x)=(k_x+k_0)+m$ for $k_x<0$. When $k_x=-k_0$, one has $m<0$. A smooth connection in between, we will have a conductive edge (two ends in the 1D structure), right?

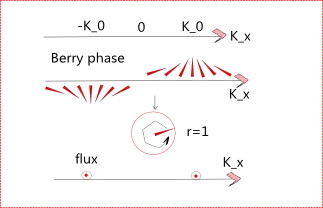
If I want to make a intuitive picture like below, is it correct? enter image description here

Any suggestion for real materials show this behavior?

Community
  • 1
Z.Sun
  • 699

1 Answers1

11

Topological insulators are gapped states of free fermions with particle number conservation and time-reversal symmetry. According to the K-theory classification, there is no Topological insulator in 1D.

However, 1D interacting fermions with time-reversal symmetry do have non-trivial symmetry protected topological phases if the particle number is conserved only mod n. The result can be obtained from group cohomology theory arXiv:1106.4772 of Chen, Gu, Liu, and Wen.

Xiao-Gang Wen
  • 13,725