Fluid rotating in theta direction in a tank

Question

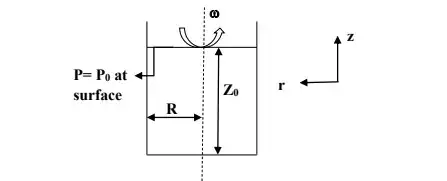
A Newtonian fluid of constant density $\rho$ is in a vertical cylinder of radius R with the cylinder rotating about its axis at angular velocity $\omega$. Find the shape of the free surface at steady state.Consider the cylindrical coordinate system for analysis. Consider the pressure (P) to be a function of two coordinate system r and z. Refer to the figure below for more details.

I used Navier Stoke's equation in the angular direction since the principal motion is in ${\theta}$ direction.

$$\begin{aligned} &\theta \text { -component: }\\ &\rho\left(\frac{\partial u_{\theta}}{\partial t}+u_{r} \frac{\partial u_{\theta}}{\partial r}+\frac{u_{\theta}}{r} \frac{\partial u_{\theta}}{\partial \theta}+\frac{u_{r} u_{\theta}}{r}+u_{z} \frac{\partial u_{\theta}}{\partial z}\right)\\ &=-\frac{1}{r} \frac{\partial P}{\partial \theta}+\rho g_{\theta}+\mu\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{\theta}}{\partial r}\right)-\frac{u_{\theta}}{r^{2}}+\frac{1}{r^{2}} \frac{\partial^{2} u_{\theta}}{\partial \theta^{2}}+\frac{2}{r^{2}} \frac{\partial u_{r}}{\partial \theta}+\frac{\partial^{2} u_{\theta}}{\partial z^{2}}\right] \end{aligned}$$

Reducing it with assumptions I get

\begin{aligned} 0=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{\theta}}{\partial r}\right)-\frac{u_{\theta}}{r^{2}} \end{aligned}

\begin{aligned} c=\left(r \frac{\partial u_{\theta}}{\partial r}\right)-\int\frac{u_{\theta}}{r} dr \end{aligned}

Now it's clear that in order to solve it I have to integrate it twice, i.e., consider $u_{\theta}$ not a function of $r$. But physics bites me from inside. Can someone provide me a logic to this? Another thing is why $u_{\theta} = r \omega$ i.e., ( $sin (\theta) = 1 $) not valid here?

Answer 1

Using Navier-Stokes is taking a steamroller to crack a nut.

Your fluid is roting as a solid body so $v_\theta =r\omega$. You can find the shape of the surface by observing that in the fluid is stationary in the rotating frame, and in that frame the potential energy is $$ V(r,z)=\rho g z- \frac 12 \rho \omega^2 r^2, $$ a sum of the gravitational and centrifugal potentials. The surface must be an equipotential, so $$ z(r)= \frac 1{2g} \omega^2 r^2, $$ which is a parabola of revolution.

Your original problem askes you to use the pressure. Euler (divided by $\rho$) tells us that $$ \frac{\partial {\bf v}}{\partial t}+ \left({\bf v}\cdot \nabla \right) {\bf v}= - \frac 1 \rho \nabla P- {\bf g} $$ Now ${\bf v}=(-\omega y, \omega x, 0)$ so $$ \left({\bf v}\cdot \nabla \right) {\bf v}= -\frac 12 \omega^2 \nabla (x^2+y^2) $$ so $$ \nabla\left(\frac P\rho - \frac 12\omega^2 r^2 +gz\right)=0. $$ Thus again $P$ is constant on $$ z= \frac 1{2g}\omega^2 r^2. $$