A permanent cylindrical magnet with diameter $D$ and length $L$ possesses an uniform magnetization $\mathbf{M}$ going in the $z$-direction in a cylindrical coordinate system. The magnet is placed with its centre in the origin, with its length going along the $z$-axis.
Problem
Given the expression for the magnetic field along the $z$-axis $$\mathbf{B}(z)= \mathbf{a_z} \cdot \frac{\mu_0M}{2} \Bigg[ \frac{z+ \frac{L}{2}}{\sqrt{\big(z+\frac{L}{2} \big)^2+ \big(\frac{D}{2} \big)^2}}- \frac{z- \frac{L}{2}}{\sqrt{\big(z-\frac{L}{2} \big)^2+ \big(\frac{D}{2} \big)^2}} \Bigg] $$ arrive at an expression for the $\mathbf{H}$-field along the $z$-axis. What is the direction of $\mathbf{H}$ inside and outside the magnet?
My attempt
Given the simple relation $\mathbf{H}=\frac{\mathbf{B}}{\mu_0}-\mathbf{M}$ we get
$$\mathbf{H}(z)=\mathbf{a_z} \cdot \frac{M}{2} \Bigg[ \frac{z+ \frac{L}{2}}{\sqrt{\big(z+\frac{L}{2} \big)^2+ \big(\frac{D}{2} \big)^2}}- \frac{z- \frac{L}{2}}{\sqrt{\big(z-\frac{L}{2} \big)^2+ \big(\frac{D}{2} \big)^2}} \Bigg]-M \cdot \mathbf{a_z} $$
But I'm not sure how to answer what direction $\mathbf{H}$ has inside and outside the magnet.
Edit
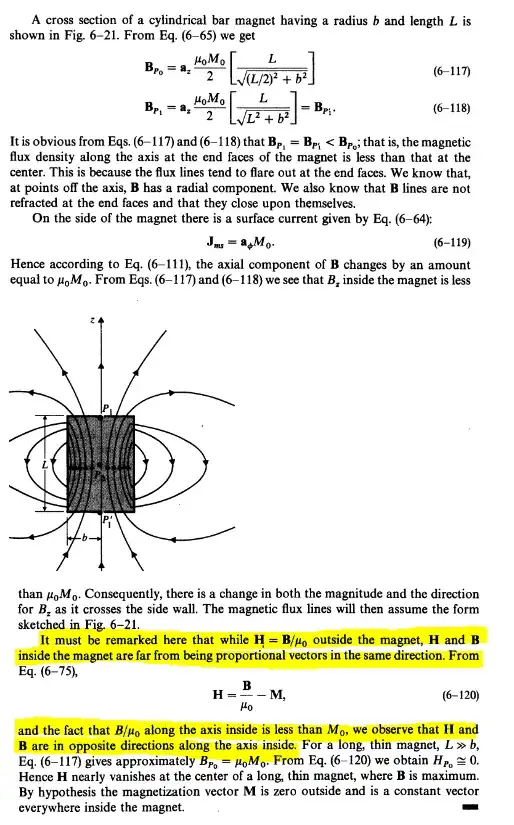
I found this example in my book, that revolves around the exact same scenario, a cylindrical magnet with uniform magnetization $\mathbf{a_z}M_0$. In the example, the author writes about the relationship about $\mathbf{H}$ and $\mathbf{B}$. He also talks about their direction, which I have marked with yellow.
So if the scenario is the same, doesn't the example answer also answer my problem completely?