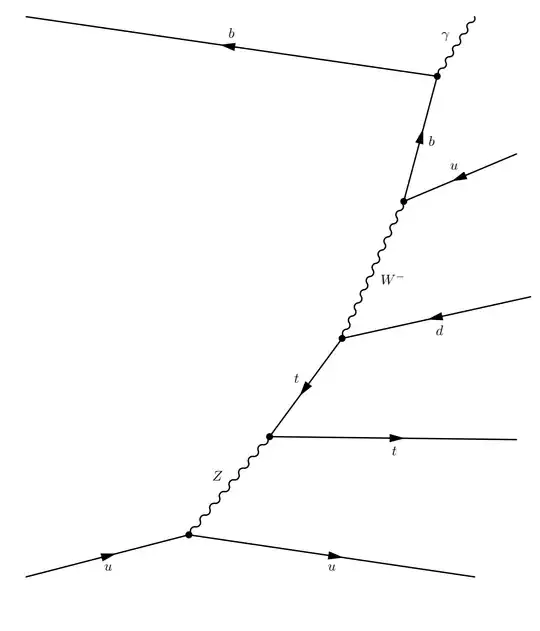
From reading the answer in Difference between the CKM and the PMNS matrix , I gather that the transition $W\to ub$ where $u$ and $b$ mean flavour eigenstates is not possible, but it is possible where $u$ and $b$ means mass eigenstates. Is this understanding correct?
If this is so, then starting with a $B+$, which is in a flavour eigenstate of $u\bar b$, not a mass eigenstate (again is this correct?) then is the following Feynman diagram possible? I believed it was, but if the $b$ that comes from the $W$ is not a flavour eigenstate, then surely the annihilation vertex at the top of the diagram $b\bar b \to y$ is not possible, as electromagnetism does not change flavour and hence requires that both the $b$ and $\bar b$ are flavour eigenstates?