The reference frame of the ship is non-inertial, so the positioning of the navigator and the captain with respect to the acceleration direction matters.
By the equivalence principle, the ship's reference frame will look the same as being on the surface of a planet with a very strong surface gravity (51 thousand $g$s with the acceleration you have given!).
So, there will be time dilation! This, however, is only as long as there is spacing between the navigator and the captain along the acceleration axis. If this distance is $h$ then the time-dilation can be expanded in powers of $ah / c^2$, where $a$ is the acceleration. As long as $h$ is of the order of single meters this is very small so only the first term matters, so there will be dilation expressed by the formula:
$$
\Delta t_N = (1 - ah/c^2) \Delta t_C
\,.
$$
If the navigator is "above" the captain, it will appear "blueshifted": the impulses it sends will seem closer to each other to the captain.
This would be your option 2: note, however, that if the captain is "above" the navigator the effect works in the opposite direction, and the pulses will be more spaced.
Anyway, the formula is always linear.
All of this applies from the beginning, there is no need for the speed to approach $c$; as other answers clarified accelerations do not work as in Newtonian mechanics for relativistic speeds.
This idea of acceleration, however, works well enough if we interpret it as a Taylor expansion near $v/c=0$.
Since speeds are relative, the effect will be the same as long as the engines of the spaceship keep applying the same thrust and as long as the navigator sends impulses which are equally spaced in time.
As the speed increases, even with constant thrust the multiples of $0.1c$ will not be reached linearly.
A reasonable form for the position as a function of time of an object with constant acceleration is
$$
x(t) = \frac{c^2}{a} \left(\sqrt{1 + \frac{a^2 t^2}{c^2}} - 1\right)
$$
so the velocity looks like
$$
v(t) = \frac{at}{\sqrt{1 + a^2 t^2 / c^2}}
$$
which, as you can see, approaches $c$ asymptotically for large $t$, but never reaches it.
For small $t$, it is a good approximation to say $v = at$.
Edit:
Since you're asking about perception, let us explore this a bit further, starting from the expression I wrote for the velocity.
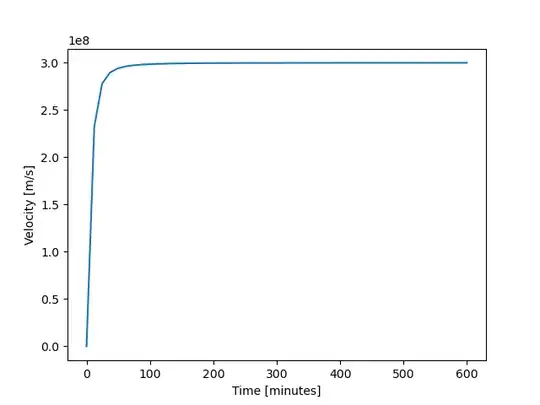
Here is a plot of it, you can see that even though the acceleration is constant the speed approaches $c$ asymptotically.
However, there is an important effect we must consider, which is the reason why this might seem weird: length contraction.
An observer moving at a certain velocity will see objects contracted along the direction of motion by a factor
$$
\gamma = \frac{1}{\sqrt{1 - v^2 / c^2}}
\,.
$$
So, even though the speed approaches $c$, the distance elapsed per second in the reference frame of the Earth (or anyhow, the frame in which the rocket started) can be larger than $c$.
Here is a plot of how $\gamma$ looks, for the same times as the velocity plot:
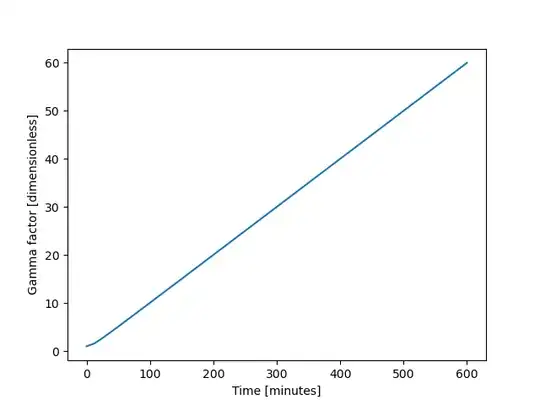
You can see that as the speed approaches $c$ this becomes quite large.
When we are to compute the distance elapsed in the Earth frame, we must use a sort of "effective velocity", computed as $\gamma v$: this can be much larger than $c$.
The velocity cannot increase further than $c$, so length contraction "picks up the slack": lengths are contracted ever further, so from the perspective of the rocket things whiz by at almost $c$, but they are much shorter so the speed referred to the Earth-frame length would be $>c$.
This effective velocity $\gamma v$ does indeed increase linearly with $\gamma v = at$, as one might expect.
This is all done under the assumption that $a$ is constant, and here $a$ is a proper acceleration: the thrust of the engine, if you will.
Thus, an observer in the ship would perceive uniform acceleration.
The "photon frame" does not exist, but what could exist is the frame of an observer moving with very large $\gamma v \gg c$: they would see stationary objects as very contracted along the axis of motion, and moving very slowly.
Such an observer would be able to travel between stars (separated by $d$) in a very short subjective time ($d / \gamma v$), while the time they take as measured by observers static with respect to the stars would be bounded by $d /c$.

