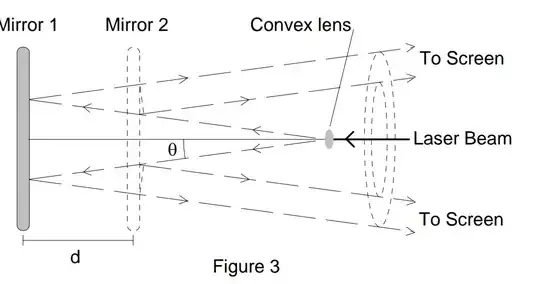
All textbooks say that the path difference is $2d \cos \theta$. But in my mind, by constructing triangles, I seem to get $2d/\cos \theta$ and intuitively I thought as angle increases, the path difference should also increase. And when angle is $90°$, path difference should be infinite. Think something is fundamentally wrong with the way I am thinking.
The key point here I think is that the path difference must be calculated at a wavefront, which is orthogonal to the rays.
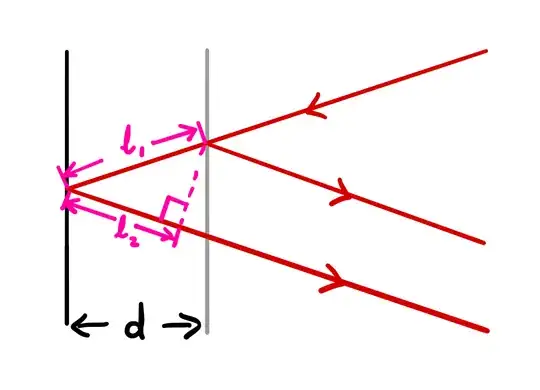
See the diagram below and note that the path difference is $\ell_1 + \ell_2$ instead of $2\ell_1$.
$\ell_1 = \dfrac{d}{\cos\theta}$ indeed, but $\ell_2 = \ell_1 \cos(2\theta)$.
Therefore, $$\Delta = \ell_1 + \ell_2 = \left(1+\cos(2\theta)\right)\ell_1 = (1 + \cos^2\theta - \sin^2\theta)\ell_1=2\cos^2\theta \;\ell_1 = 2d\cos\theta$$
The formed fringes are "fringes of equal inclination".
See
Note that here we assume the refractive index is universally $1$ (or at least uniform in the space), which is true for Michelson interferometer. For more general cases, e.g. thin film interference, the path difference is $2 n d\cos\theta$. See here for the derivation.
