Did we just misunderstand gravity?

Question

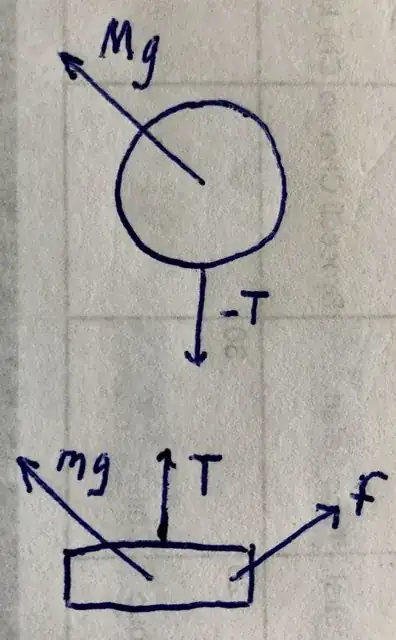
Einstein told us that a spring balance under free fall shows zero deflection and thus derived that gravity is a curvature in the fabric of spacetime and all those stuffs.

Now let's assume we have a spring balance in gravity-free space (though there is a gravitational force between me and the balance) as shown below. If we somehow apply a horizontal force on the hook or pan using my fingers and with no opposing force on the spring, it starts accelerating in the direction of the force. Will the pointer show any deflection ?

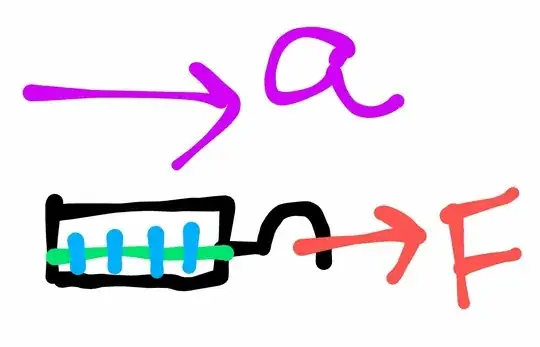
No, and to get any deflection we need to apply another force in the opposite direction so that it doesn't accelerate and the spring inside the balance gets stretched ¹.

So does it mean that all forces are pseudo forces like gravity or we just misunderstood gravity? Doesn't this experiment signify that all forces have some common feature? Or am I wrong somewhere?

1 : In this question OP mentioned that when the other end of a spring balance is free, it shows zero deflection.

Answer 1

If we apply an unbalanced force to the spring balance and another unbalanced force to the mass attached to it so that both spring balance and mass have the same acceleration then the spring balance will not show any deflection.

But if we apply an unbalanced force to the spring balance and no external force to the mass attached to it then the length of the spring in the spring balance will change and the spring balance will show a deflection.

... we need to apply another force in the opposite direction such that the spring inside the balance gets stretched

No, I don't think this is correct.

Answer 2

If we apply a force on the pan using my fingers and with no opposing force, it starts accelerating in the direction of the force. Will the pointer show any deflection?

Yes. In fact, the pointer will show a deflection which is proportional to the force applied. The exact deflection depends on the mass of the pan, the spring, and the body of the spring balance. The more massive the body and the less massive the pan and the spring the greater the fraction of the force will be detected. What matters is how much the spring stretches, and by accelerating the pan it will stretch some.

See the free body diagrams below. The circle is the body of the scale, mass $M$, and the rectangle is the pan, mass $m$. The spring has a tension $\vec T$ and is assumed to have negligible mass. An external force $\vec f$ is applied to the pan and the scenario is analyzed from a reference frame which is accelerating at $-\vec g$. The inertial forces are parallel, and the tension forces are anti parallel. No other special directions are assumed.

After any initial transients die out the steady state is when the body and the pan have equal acceleration $\vec a$. Writing Newton’s 2nd law for the body and the pan gives $$ M \vec g -\vec T= M \vec a$$ $$m\vec g +\vec T +\vec f=m\vec a$$ Solving these for $\vec a$ and $\vec T$ gives $$\vec a= \frac{\vec f}{M+m}+\vec g$$ $$\vec T=-\frac{M}{M+m} \vec f$$

Note that the reading on the scale, $\vec T$, is proportional to $\vec f$ but does not depend on $\vec g$. So regardless of the acceleration of the reference frame (including $-\vec g=0$) the steady state reading on the scale depends only on the force applied.

Note also that the form of the inertial force is the same as the form of a uniform gravitational force. So the same conclusions apply to a Newtonian inertial frame in the presence of a gravitational field. The reading on the scale is independent of gravity.

Answer 3

If I understood correctly, it is the same as to apply a force on a massive spring. It will deflect according to Hooke's law while the force is there. And it will have an acceleration $a = \frac{F}{m}$.

Answer 4

Indeed the spring balance will show deflection.

You can think of it like this:

When you start applying force at one end of the spring balance then due to the principal of locality (whic means that any force will affect only it's immediate surrounding) only the nearest particle will accelerate. But since the the spring is made up of particles linked via intermolecular forces therefore this force will propagate through the medium of the spring (at the speed of sound) and rest of the spring will start gaining velocity too. But before each particle starts applying force on the next particle it would have moved a bit ahead of its original position (with respect to the rest of the particles). This will lead to the expansion of the material of spring balance.

---

Aside

From this you can easily see that if you accelerate the object above certain limit such that the intermolecular forces cannot match-up with then the material of the spring balance will first inelastically expand at certain point and then break-off.