How to calculate the strength ("space force") of dark matter within galaxies?

Question

Let's first have a look at the observed speed within galaxies (source):

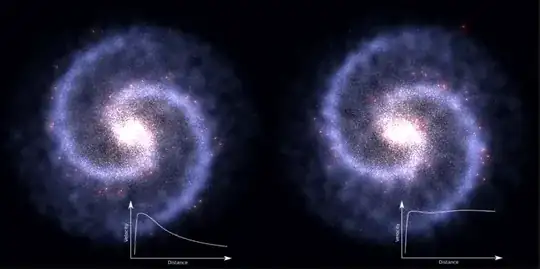
On the left side we can see the speed of celestial bodies within galaxies derived by gravity only (gravity is usually created by a black hole at the center of a galaxy), on the right side we can see the observed speed of celestial bodies, both in respect of the distance from the galactic center.

As a result, the strength of dark matter (or "space force") could be calculated as:

$F$_{dark matter} = $m$_galaxy $\cdot$ $v$_{celestial body within galaxy} $\frac{d}{dt}$ - $g$_{black hole, center of galaxy}

Is this a viable calculation? And if so, are there any a graphs online which show this strength of dark matter (or "space force") in respect of the distance from the galactic center?

(Note: In this formula, a galaxy would be assigned a mass $m$_galaxy much higher than the mass of its black hole. However, mathematically speaking one could also just decrease $dt$, so with a celestial body wandering from the center to the outskirts of the galaxy, $dt$ would decrease, hence the speed of time would increase. I doubt this is true because it would change the basic definition of speed $v$_{celestial body within galaxy} as well and introduce all kinds of illogical contradictions, but in math everything is possible as we know from theory of relativity...)

Addendum:

• $m$_galaxy $\cdot$ $v$_{celestial body within galaxy} $\frac{d}{dt}$ $[kg·\frac{m}{s^2}]$ = observable force (shown in picture on the right)
• $g$_{black hole, center of galaxy} $[kg·\frac{m}{s^2}]$, the force caused by gravity of a black hole (shown in picture on the left)
• $F$_{dark matter} $[kg·\frac{m}{s^2}]$, the force of dark matter up until a point in space

Answer 1

Your equation seems to be trying to express the gravitational contribution of dark matter as the difference between the observed gravitational force on a star at a given distance from the centre of a galaxy and the theoretical gravitational force based on the stars that can be seen in the galaxy.

This is pretty much what the velocity/distance curves show. The difference between observed and theoretical gravitational force can be worked out from the rotational velocity at a given distance because the centripetal force required to keep a star in a galactic orbit with speed $v$ and radius $r$ is proportional to $\frac {v^2}{r}$.

The super-massive black hole which lies, we believe, at the centre of most galaxies makes only a very small contribution to the gravitational attraction of the galaxy as whole. The typical mass of such a black hole is around $1 \%$ of mass of the stars in the galaxy, or around $0.1 \%$ of the total galactic mass including dark matter.