What developments have been made in this unsolved problem?

Question

I found this section in The Feynman Lectures Vol. 1 page (28-2). I was curious on where we stand to solve this question as of today? Any information/links on developments will be helpful.

\begin{equation} \tag{28.3} E=\frac{-q}{4\pi\epsilon_0}\left[ \frac{e_{r'}}{r'^2}+\frac{r'}{c}\,\frac{d}{dt}\left( \frac{e_{r'}}{r'^2}\right)+\frac{1}{c^2}\,\frac{d^2}{dt^2}\,e_{r'} \right]. \end{equation} ...

For those purists who know more (the professors who happen to be reading this), we should add that when we say that (28.3) is a complete expression of the knowledge of electrodynamics, we are not being entirely accurate. There was a problem that was not quite solved at the end of the 19th century. When we try to calculate the field from all the changes including the charge itself that we want the field to act on, we get into trouble trying to find the distance, which is zero. The problem of how to handle the part of this field which is generated by the very charge on which we want the field to act is not yet solved today. So we leave it there; we do not have a complete solution to that puzzle yet, and so we shall avoid the puzzle for as long as we can.

Answer 1

In a way, yes, but not completely. Feynman probably knew very well about it... but some of it happened after those lectures.

Perturbative renormalization

In the years following the birth of QED, it became quickly obvious that parameters (masses and charges, coupling constants) in the lagrangian couldn't be directly the physical quantities that we know. Feynman and others found a way to handle the problem, called perturbative renormalization, which is an ad hoc process using Feynman diagrams to classify all possible behaviors of a system, including self-interaction of a particle with itself.

The idea is that, in QED, the most basic interaction involves an electron and a photon or, more precisely, two electronic entities (two electrons, or two positrons, or one of both) and a photon. For example:

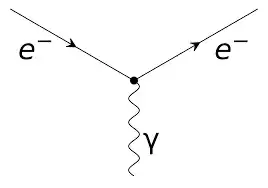
This is an electron emitting or absorbing a photon and continuing on its way from left to right. This could be a part of:

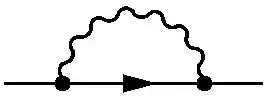
which is an electron emitting a photon and reabsorbing it later on. This second diagram is an example of self interaction.

For each diagram, you can define its order as the number of three-branch vertices like the first example above. Roughly speaking, each vertex generates a probability amplitude proportional to the fine structure constant $\alpha$. The process is called perturbative because, as you generate more and more diagrams, you build an expansion in powers of $\alpha$.

In other words, perturbative QED gave a way to study self-interaction of the electron with its own electromagnetic field, by listing diagrams where an electron emits a photon, and then this photon can generate an electron-positron pair... and so on... until all is reabsorbed by the electron.

What is the problem?

When he did those lectures, Feynman obviously knew all this. He also knew that the process above is based on the fact that $\alpha$ is small so that, hopefully, focusing on diagrams with small numbers of vertices can yield useful results (like a Taylor expansion where you keep only the first few terms).

There was no guarantee that this approximation would give the whole story, and it didn't work as well with other field theories like QCD.

What progress were made afterwards?

In the 70's (after Feynam's lectures), something called the renormalization group was devised, and non-perturbative renormalization was starting to gain traction. So new understanding about self-interaction was made.

It became clearer that it was not possible to define the electron (or the photon, and so on) without specifying an energy scale $\Lambda$, also called cutoff. Remebering that an energy scale is inversely proportional to a distance scale:

• All self-interactions involving energy higher than $\Lambda$ are "integrated out" and part of the definition of the electron.
• In other words, "small details" are part of the internal structure of this electron and aren't visible from the outside.

The renormalization group is the idea that, starting from a hypothetical "naked" electron (infinite energy scale, or zero-distance scale), we can reduce $\Lambda$ (backing away with the camera, so to speak) little by little, integrating more and more self-interaction inside the electron in the process.

During the process, what we call electron changes, as more and more self-interaction is embedded inside it. Its mass and charge change. When $\Lambda$ becomes small enough, the resulting electron becomes the one that we've known for a century, with its well-known mass and charge.

So, is it a solved problem?

Not really. The mathematical problem is huge and, as far as I know, not completely solvable. Non-perturbative renormalization is still an active field of research.

The best quantum field theory can give us is effective theories: theories that are valid for a given energy scale $\Lambda$. And trying to take the limit $\Lambda\to+\infty$ is useless, as this is equivalent to removing renormalization, so you get infinite values for mass or charge. In other words, the "naked electron" is a theoretical construct, but probably not something that can exist.

It means that, if there's a theory capable of describing an electron at extremely high energy, we haven't found it yet. It means that we don't know how to study high-energy self interaction properly.