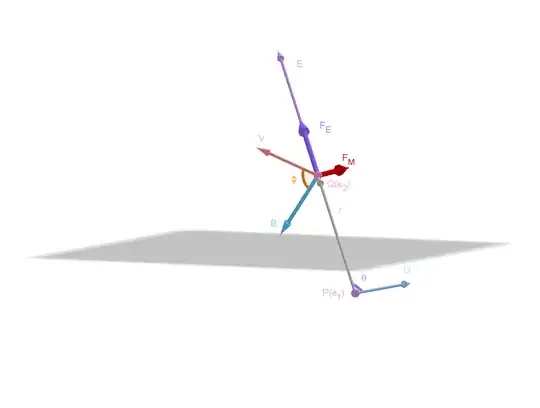
Consider two electrons $e_1$, $e_2$, located at $P_{xyz}$ and $Q_{xyz}$, with velocities $u_{xyz}$ and $v_{xyz}$ respectively in the observer's inertial frame of reference, both with charge $e$.
I wish to determine the instantaneous electro-magnetic forces exerted by $e_1$ on $e_2$. I understand that I firstly need to calculate the Electric Field vector $\bf{E_{1Q}}$ and the Magnetic Field vector $\bf{B_{1Q}}$ which both occur at position Q due to the influence of electron $e_1$.
Secondly I need to determine (and then vector-sum) the forces exerted by those fields on the second electron $e_2$.
From this wikipedia article: Biot-Savart Law (section: "Point charge at constant velocity") I obtain expressions (derived by Oliver Heaviside, 1888, from Maxwell's Equations) for the Electric Field vector $E_{1Q}$ and the Magnetic Field vector $B_{1Q}$:-
$$ \bf{E_{1Q}} = \frac{e}{4\pi\epsilon_0} \frac{1-\frac{u^2}{c^2}}{\left(1-\frac{u^2}{c^2}\sin^2\theta_{ur}\right)^{3/2}}\frac{ \hat{r} }{\lvert r\rvert^2}$$
where $r$ is the displacement vector $r = Q_{xyz}-P_{xyz}$ ,$\hat{r}$ is the unit vector of $r$ and $\theta_{ur}$ is the angle between $e_1$'s velocity $u_{xyz}$ and $r$.
$$ \bf{B_{1Q}} = \frac{\textbf {u} \times \bf{E_{1Q}} }{c^2} $$
(where $\times$ is the vector product operator).
Next I can find the force $\mathbf{F_m}$ exerted by the magnetic field upon electron $e_2$ from the equation:-
$$\mathbf{F_m} = e \left( \bf{v} \times \bf{B_{1Q}} \right)$$
where the direction of $\mathbf{F_m}$ is obtained from Fleming's left-hand Motor rule.
However I am unclear as to how to calculate the force $\mathbf{F_E}$ exerted by the electric field upon target electron $e_2$. My textbook only gives the equation for the Coulomb force ($\mathbf{F_c}=e.\mathbf{E}$) exerted by an electric field on a static electron. I presume that the target electron velocity $\mathbf{v_{xyz}}$ needs to be taken into account somehow. Please can somebody tell me how?
UPDATE
As tomtom1-4 answered, I can use the Lorentz Force equation, which in SI units is:-
\begin{equation} \mathbf{F} = e ( \mathbf{E} + \mathbf{v} \times \mathbf{B}) \end{equation}
which is equivalent to:-
\begin{equation} \mathbf{F} = e ( \mathbf{E} + \mathbf{v} \times \frac{\textbf {u} \times\bf{E} }{c^2}) \end{equation}
\begin{equation} \mathbf{F} = e ( \mathbf{\hat{r}} \vert E\vert + \mathbf{v} \times \frac{\textbf {u} \times \mathbf{\hat{r}} \vert E\vert }{c^2}) \end{equation}
\begin{equation} \mathbf{F} = e \vert E\vert \left( \mathbf{\hat{r}} + \frac{1}{c^2} \mathbf{v} \times (\textbf {u} \times \mathbf{\hat{r}} ) \right). \end{equation}
Substituting for $\vert E \vert$ using the Heaviside expression for $E_{1Q}$ gives:-
\begin{equation} \mathbf{F} = \frac{ee}{4\pi\epsilon_0 r ^2} \left[\frac{1-\frac{u^2}{c^2}}{\left(1-\frac{u^2}{c^2}\sin^2\theta_{ur}\right)^{3/2}}\right] \left( \mathbf{\hat{r}} + \frac{\mathbf{v} \times (\textbf {u} \times \mathbf{\hat{r}} )}{c^2} \right). \end{equation}
For comparison here is the formula from Thomas Fritsch's (Darwin-based) answer:- $$\mathbf{F}=\frac{ee}{4\pi\epsilon_0r^2} \left(\hat{\mathbf{r}} + \frac{ \mathbf{u}(\hat{\mathbf{r}}\cdot\mathbf{v}) +\mathbf{v}(\hat{\mathbf{r}}\cdot\mathbf{u}) -\hat{\mathbf{r}}[\mathbf{u}_1\cdot\mathbf{v}+3(\mathbf{u}\cdot\hat{\mathbf{r}})(\hat{\mathbf{r}}\cdot\mathbf{v})] }{2 c^2} \right).$$
As per Ján Lalinský's comments, I'm beginning to see how, even in Galilean relativity, timing considerations make the situation I describe more complicated in terms of the time-variant E & B fields at point Q than they would be in the case of, for example, a Biot-Savart steady current element at point P.