If you are learning about the Kerr geometry I strongly recommend Matt Visser's paper The Kerr spacetime: A brief introduction as he manages to pack in all the essential information and still keep it readable.
The location of the ergosphere is derived by considering the trajectory of an observer at constant $r$, $\theta$ and $\phi$, and requiring that this trajectory be time like. With a bit of fiddling this comes down to the condition that $g_{00} < 0$ and using the Boyer Lindquist coordinates this gives us:
$$ r^2 − 2mr + a^2 \cos^2\theta < 0 \tag{1} $$
The ergosphere is where the left side above is equal to zero, and since this is a quadratic in $r$ solving it gives us two ergosphere boundaries:
$$ r_e^\pm = m \pm \sqrt{m^2 - a^2 \cos^2\theta } $$
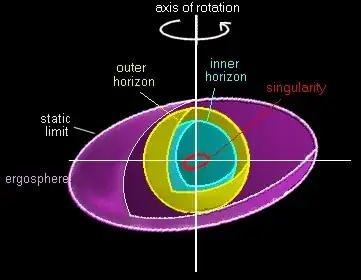
The radius $r_e^+$ is the outer ergosphere and $r_e^-$ is the inner ergosphere. It is the region in between these two radii where it is impossible to remain at constant $r$, $\theta$ and $\phi$. Note that:
$$ r_e^+ \ge r^+ \ge r^- \ge r_e^- $$
i.e. the outer ergosphere lies outside the outer horizon and the inner ergosphere lies inside the inner horizon. So if you start far from the black hole you can hover at constant $\phi$, then as you reach the outer ergosphere you find this is no longer possible. As you keep going inwards you pass through both horizons then eventually reach a radius where you can once again hover at constant $\phi$, and that's the inner ergosphere.
Or you could look at this the other way round: starting from the centre and moving outwards you can hover at constant $\phi$ until you reach the inner ergosphere and above this you cannot hover at constant $\phi$ until you've passed through the outer ergosphere.
Finally I should add the obligatory caveat that the Kerr metric is an ideal case and is probably unstable inside the outer event horizon. A real rotating black hole would probably have a different, and currently unknown, internal geometry.