Why do people use real values for the Wick-rotated time $\tau$?

Question

In doing instanton problems or when connecting quantum field theory to statistical mechanics, I often see people trying the Wick rotation trick by defining an imaginary time $\tau\equiv it$. So, in this case, we should make sure that $\tau$ is imaginary, right? However, I often see places where people seem to handle $\tau$ as a real number, for example setting $\tau$ to $\pm\infty$. Moreover, I remember in one of my quantum mechanics classes, the professor said the Euclidean time $\tau$ was real. I am so confused and need some good explanations.

Answer 1

1. Wick rotation is more than just a change of time coordinate from $t_M\in\mathbb{R}$ to $t_E=it_M\in i\mathbb{R}$, cf. e.g. this related Phys.SE post. It the assumption that we can analytically extend the time coordinate to the complex plane $\mathbb{C}$ (minus possible poles and branch cuts), and use complex function theory and Cauchy's integral theorem to deform the time integration contour from the real to the imaginary time axis, or vice-versa.

2. Wick rotation is mainly used to turn an oscillatory Minkowski path integral into an exponentially damped Euclidean path integral, which is mathematically better behaved.

Answer 2

In order to explain what a Wick rotation is all about I take an example of a computation of the one-loop correction of the electron-photon vertex that is (for instance) documented in Peskin & Schroeder chap. 6.2. I will only show the extract of the calculation where the Wick rotation is applied. In order to show how it works I've added a picture ( the black dots represents the poles of the integrand for this example):

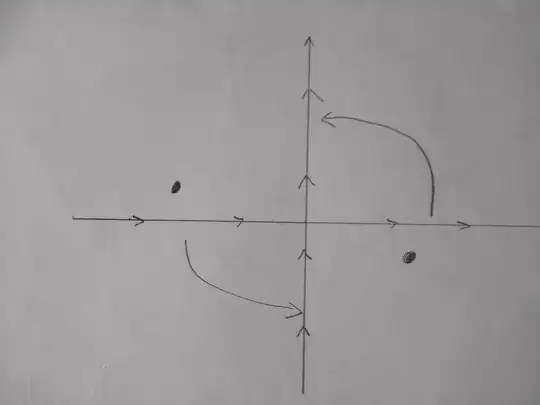First of all, the concerned integral has to be considered as complex contour integral whose path is actually closed by a line in the upper half-plane that connects $\infty$ with $-\infty$ by a large arc that lays at infinity. Actually, in this step one has already to make sure that such an extension of the integration path is possible without changing the integral in question, i.e. that the integrand falls rapidly off at complex infinity in the upper half-plane.

The next step consists of changing the integration path by a rotation of $90^\circ$ -- the actual Wick rotation. In order to allow for such a change of integration path one has to assure that the integrand falls sufficiently rapidly off for $l^0\rightarrow \infty$ and that the new contour surrounds the same poles of the integrand as for the original contour.

$$\int^{\infty}_{-\infty} dl^0 \int \frac{d^3 l}{(2\pi)^4} \frac{1}{[l^2-\Delta]^3} \stackrel{contour\, change}{=} \int^{i\infty}_{-i\infty} dl^0 \int \frac{d^3l}{(2\pi)^4} \frac{1}{[l^2-\Delta]^3}$$

The final step consists of a redefinition of the variables $l_0$ and $l_{1,2,3}$ to Euclidean ones:

$$ l^0 = il^0_E \quad \quad\text{and}\quad\quad \mathbf{l} = \mathbf{l_E}$$

Applied to the integral it yields ($l^2 = (l^0)^2 -\mathbf{l}^2 = -(l^0_E)^2 -\mathbf{l_E}^2=:-l_E^2$):

$$\int^{i\infty}_{-i\infty} dl^0 \int \frac{d^3 l}{(2\pi)^4} \frac{1}{[l^2-\Delta]^3} =\frac{i}{(-1)^3}\int^{\infty}_{-\infty} dl^0_E \int \frac{d^3 \mathbf{l}_E}{(2\pi)^4} \,\frac{1}{[l^2_E + \Delta]^3}$$

where on the rhs of the equation the generated common minus sign (to the cube) was factored out of the denominator.

Recap: a Wick rotation consists of 2 essential steps: Extension the original integration path to a closed contour on the complex plane and rotation by $90^\circ$. Second step: substitution of the now complex variable that parametrises the integration path by a real one.