I'm studying the Nishinaka-Yoshida crystal models that encode the generating function of $D4$-$D2$-$D0$ BPS bound states on a Calabi-Yau divisor.
The case of conifold at its singular point is developed in Statistical model and BPS D4-D2-D0 counting and the case $A_{N-1} \times \mathbb{C}$ is discussed in A note on statistical model for BPS D4-D2-D0 states.
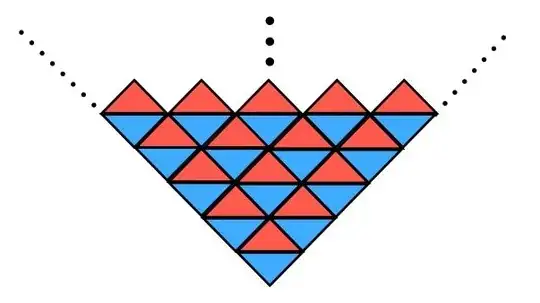
The paper that dicuss the conifold case explicitly states that the completely "frozen" crystal (the triangular partition without "triangular atoms" removed) is identifyed as a $D4$-wrapping the conifold. The picture in the above shows the frozen crystal.
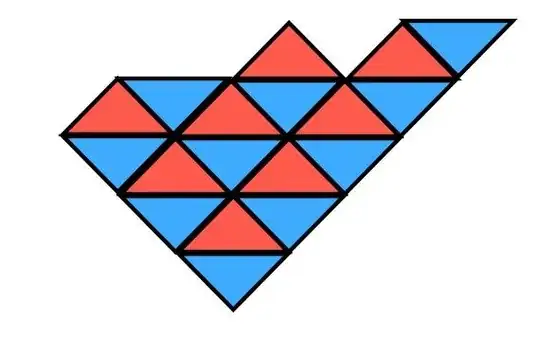
A general crystal melting configuration must have atoms removed and should represent a general $D2$-$D0$ bound state "sticked" to the $D4$ brane. The following picture shows an example.
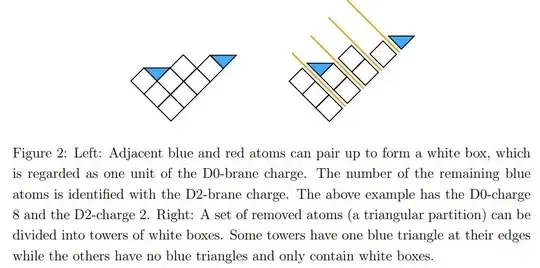
The authors show that if one identify blue triangles as one unit of $D2$-brane charge and pairs of red and blue triangles as white boxes representing one unit of $D0$ brane charge, then his model is able to compute the desired BPS index.
I'm unable to see the rationality behind those choices, they seem totally arbitrary to me (beyond the fact that the identifications are needed to reproduce the desired partition function).
Questions:
How can I derive those choices from first principles?
Is there any direct relation with the two dimensional Calabi-Yau crystals constructed in Crystals, instantons and quantum toric geometry?
Thanks in advance.