0

In my book, I read that we can choose any level as Zero Gravitational P.E. and measure height of objects above it and call its energy 'mgh'. But by saying that all the points on that level is of zero potential, it can be inferred that it is an Equipotential surface but we know that all the points have different potentials (I know , a concentric sphere around earth is an equipotential surface but we often choose zero level that is not earth's surface )

Please explain as it is really confusing me :)

Qmechanic
  • 220,844
Aryaman
  • 5
  • 1

1 Answers1

1

In my book, I read that we can choose any level as Zero Gravitational P.E. and measure height of objects above it and call its energy 'mgh'.

This works because we're almost always only interested changes in potential energy, rather than absolute values.

Let me show below that the reference point is of no importance in that case.

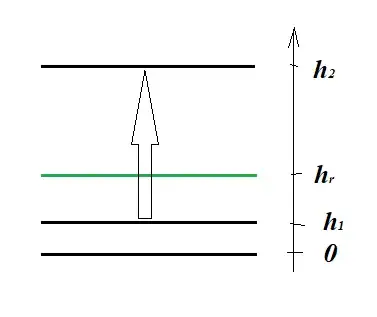
Potential energy

Let $h_r$ be a reference point where $U=U_r$. You can assume $U_r$ to be unknown. Now we look at an object of mass $m$ that is moved from $h_1$ to $h_2$ and want to know its change in potential energy.

We know that: $$U_1=U_r+(h_1-h_r)mg$$ $$U_2=U_r+(h_2-h_r)mg$$ The change $\Delta U$ is: $$\Delta U=U_2-U_1=U_r+(h_2-h_r)mg-[U_r+(h_1-h_r)mg]$$ $$\Delta U=mg(h_2-h_1)$$ So choosing an arbitrary, non-zero reference point gives the same, correct change in potential energy.

Another, more 'absolute' way of looking at it is by looking at the potential energy in a gravitational field$^\dagger$, far away from Earth's surface:

$$U=-\frac{GMm}{r}$$

Here obviously for $r\to +\infty$ then $U=0$. So here $r= +\infty$ is a good zero reference point.

$^\dagger$ http://hyperphysics.phy-astr.gsu.edu/hbase/gpot.html

Gert
  • 35,561