The following is a specific instance of the brachistochrone problem, which I first encountered in grad school, and I have occasionally used as hw problem in teaching CM.
A particle is started from rest at the origin and constrained to fall under gravity along a path $y(x)$ which passes through the point $x=5$, $y=-1$ (in arbitrary units, for example meters). We will assume that the gravitational potential is linear, $V=mgz$.
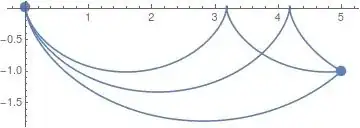
a) Determine the path that minimizes the time taken. Make a plot of that path.
b) Is there another path that makes the time taken stationary? If yes, make a plot of that path and explain whether this path is a minimum, a maximum, or a saddle point.
The solution to the brachistochrone problem is of course very well known, so this assignment is really about finding a specific cycloid that satisfies the boundary conditions. As part b indicates, there is more than one: The standard cycloid, and two cycloids that ``bounce''.
Now it is clear that the simple cycloid is the absolute minimum, because traversal time is proportional to the angle traced out. But what about the other two? Naively they should be saddles, but the second variation of the action functional is manifestly positive, indicating that they are local minima. But that can't be right, unless there is something funny about the topology of the space of paths. Are the higher cycloids saddle points or minima?
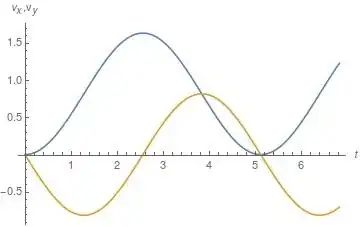
P.S.: To see that the higher cycloids cannot easily be dismissed as solutions, consider this plot of the velocity components $(v_x,v_y)$ as a function of time for the second cycloid.
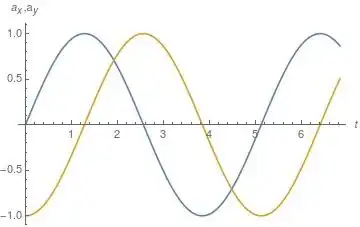
The corresponding components of the acceleration are:
Clearly, the acceleration (and the forces of constraint) are perfectly smooth.