Photons are quantum mechanical elementary particles in the very successful quantum field theory standard model. If you look at the table, they are on par with electrons, and individual photons are point particles, not waves in any space. What waves is the mathematical complex value wavefunction $Ψ$, whose only measurable prediction is the probability of finding a photon in (x,y,z,t) in space, equal to the real number $Ψ^*Ψ$ .
What you had drawn (in a previous version) was a description of a free photon as a wavepacket , in quantum field theory , and it is a probability wave packet, not a space and time wave wavepacket.
Since they oscillate regularly or continuously then why is the energy released in the form of packets ?
The premise is wrong. Individual photons do not oscillate, see this experiment with single photons at a time. It is the probability of measuring it that oscillates.
What causes this discontinuity in released energy ??
the fact that is a single particle that is carrying it.
Can we calculate the time gap between each of these photons ( which should exist when we say them as packets ), even if it is too small ??
Everything in quantum mechanics that can be calculated is probabilistic. There will be a calculable probability , depending on the source, whether an atom, or a decelerating electron or other charged particle.
As the energy of a photon is $hν$ where $ν$ is the frequency of the classical wave many thousands of photons build up (see link of single photons above) and h is a very small number, ordinary electromagnetic waves, light, emerge from zillions of photons in a way calculable with quantum electrodynamics.
Since the electrons oscillate regularly then why is the energy released in the form of packets and not continuously in the form of waves ? What causes this discontinuity in released energy by electrons ?
Free electrons, of fixed momentum, do not oscillate. Thep probability of finding them at (x,y,z,t), connected with the wavefunction, has sinusoidal behavior.
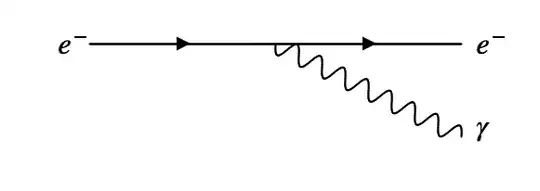
Electrons decelerated in some field, do radiate photons, i.e. elementary particles , which by their existence take energy away.
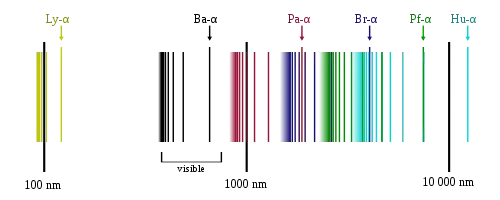
Electrons bound in the atoms do not oscillate regularly. They are quantum mechanically bound in orbitals at specific energy levels with specific quantum numbers. See the simple orbitals for electrons in a hydrogen .
Actually the discontinuity, the spectra of the atoms, is one of the basic reasons quantum mechanics was invented. See this answer of mine.