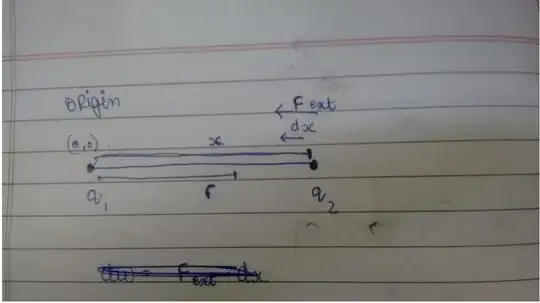
Consider a fixed, positive Point charge $q1$, kept at the origin. Another (positive) charge, $q2$, is being brought from $\infty$ to the point $(r,0)$, by an external agent slowly. We wish to calculate the work done by the external agent (and thus derive the "potential" of the point charge $q1$, being defined as $w_{ext}/q2$ (or as $-w_{electric}/q2$)). Suppose we consider a position $(x,0)$:
- The magnitude of force is going to be $kq1q2/x^2$. We will thus have, $\vec{F}=\dfrac{-kq1q2}{x^2}\hat{i}$.
- When we displace it from a position $(x,0)$ to $(x-dx,0)$, the displacement vector$(\vec{ds})$ will be $(x-dx)\hat{i}-x\hat(i)=-dx\hat{i}$.
- Using $dw$=$\vec{F}.\vec{ds}$, we will get $dw=\dfrac{kq1q2}{x^2}dx$. Upon integrating from $\infty$ (initial position) to $r$ (final position), we get : $$w_{ext}=-\dfrac{kq1q2}{r}$$ and thus $$V(r)= w_{ext}/q2 =-\dfrac{kq1}{r}$$ which is completely absurd. I tried to be as rigorous as possible with the definitions, vectors etc and yet a -ve sign has crept in somewhere.
The only issue seems to be with the treatment of $dx$. Although , I took $dx$ to be the magnitude of displacement, and accounted for the direction by using $-\hat{i}$.A possible argument seems to be "$x$ decreases, so $dx$ is a negative quantity. So the "magnitude" should be $-dx$. My two concerns:
- What is then, the issue with displacement=$\vec{r_{final}} - \vec{r_{initial}}$ that simply yields $-dx\hat{i}$?
- Simply "putting" a - sign before $dx$ after claiming "$dx$ is negative" seems to be arbitrary. There should be an argument (like I presented in the previous bullet point) that will produce the - sign for the magnitude, and thus making the vector $(-dx)(-\hat{i})$.
The main essence of this problem seems to be rigorously defining what $dx$ actually represents, for a quantity $x$.
I believe the entire thing can be summarized by one question:
What is wrong in writing displacement=$\vec{r_{final}} - \vec{r_{initial}}$ that simply yields $-dx\hat{i}$? If I had $(x+dx)$ instead of $(x-dx)$,then the derivation would be correct. But why is this the Case?