Why is maximal kinetic energy lost in a perfectly inelastic collision?

Question

A perfectly inelastic collision is one where both of the colliding objects stick together and move as one.

My question is, why, of all possible combinations of final velocities that conserve momentum, does this one lead to the greatest loss in kinetic energy?

One reasoning I found was that this is the only combination in which the total kinetic energy of the system becomes 0 in some frame of reference (com frame). But just because the KE is 0 in some frame doesn't mean that it is the least possible in every other frame, does it?

Answer 1

As far as I can tell, what we need here is an intuitive understanding rather than a mathematical one. The intuition gets a bit blurred by the mathematical expressions. But, if we take the two colliding bodies to be of equal mass, the expressions get greatly simplified. While not immediately obvious, the results apply to arbitrary combinations of masses.

Let me mass in question be $m$. If we call the initial velocities of the two bodies $\vec{v_1}$ and $\vec{v_2}$, and the final velocities $\vec{v_1'}$ and $\vec{v_2'}$ respectively, our only constraint is that momentum must be conserved. So:

$m \vec{v_1} + m \vec{v_2} = m \vec{v_1'} + m \vec{v_2'}$

Since we took the masses to be equal, this immediately reduces to:

$\vec{v_1} + \vec{v_2} = \vec{v_1'} + \vec{v_2'}$

Now, the velocity of the center of mass (sometimes we call it center of momentum, especially when dealing with relativistic systems) which we will call $\vec{V}$ is:

$ \vec{V} = \frac{m \vec{v_1} + m \vec{v_2}}{m + m}$

Again, by virtue of equal masses readily reduces to:

$ \vec{V} = \frac{\vec{v_1} + \vec{v_2}}{2}$

If we transform the initial velocities to this new frame, and call the respective initial velocities of the bodies in this (center of mass) frame $\vec{u_1}$ and $\vec{u_2}$, they are:

$\vec{u_1} = \vec{v_1} - \vec{V}$

$\vec{u_2} = \vec{v_2} - \vec{V}$

Substitiution of the expression for $\vec{V}$ yields:

$\vec{u_1} = \vec{v_1} - \frac{\vec{v_1} + \vec{v_2}}{2}$

$\vec{u_2} = \vec{v_2} - \frac{\vec{v_1} + \vec{v_2}}{2}$

Simplification leads to:

$\vec{u_1} = \frac{\vec{v_1} - \vec{v_2}}{2}$

$\vec{u_2} = \frac{\vec{v_2} - \vec{v_1}}{2}$

Ooooh... So, $\vec{u_1}$ and $\vec{u_2}$ are equal and opposite! This suggests defition of a relative velocity:

$\vec{r} = \frac{\vec{v_1} - \vec{v_2}}{2}$

Such that now

$\vec{u_1} = \vec{r}$

$\vec{u_2} = -\vec{r}$

Why all this trouble? All this work essentially shows two things:

• In the center of mass frame, the bodies have same magnitude and opposing direction velocities.

• In the original frame, the velocities can be expressed as:

$\vec{v_1} = \vec{V} + \vec{r}$

$\vec{v_2} = \vec{V} - \vec{r}$

If we call the kinetic energy in the original frame $T$, we can express it as:

$T = \frac{1}{2}m v_1^2 + \frac{1}{2}m v_2^2$

Well, $v_1^2$ is $\vec{v_1}\cdot\vec{v_1}$ and $v_2^2$ is $\vec{v_2}\cdot\vec{v_2}$. So:

$T = \frac{1}{2}m (\vec{V} + \vec{r})\cdot (\vec{V} + \vec{r}) + \frac{1}{2}m (\vec{V} - \vec{r})\cdot (\vec{V} - \vec{r})$

Let us expand this crazy thing:

$T = \frac{1}{2}m (V^2 + r^2 + 2 \vec{V}\cdot\vec{r}) + \frac{1}{2}m (V^2 + r^2 - 2 \vec{V}\cdot\vec{r}) $

Here, a minor miracle occurs. There is perfect cancellation of the dot products. This perfect cancellation only occurs when $\vec{V}$ is the velocity of the center of mass; for any other frame the cross-terms will remain. As such, the center of mass frame is special. (This works just as well when the masses are not equal, just with more complicated expressions.)

Our kinetic energy expression is now:

$T = \frac{1}{2}m V^2 + \frac{1}{2}m V^2 + \frac{1}{2}m r^2 + \frac{1}{2}m r^2 $

Now, this is really cool. The kinetic energy split itself into two distinct parts. One, we can call $T_c$, which is the kinetic energy due to the motion of the center of mass which is just:

$T_c = \frac{1}{2}m V^2 + \frac{1}{2}m V^2$

The second part, which we can call $T_r$, which is the kinetic energy due to motion relative to the center of mass:

$T_r = \frac{1}{2}m r^2 + \frac{1}{2}m r^2$

And of course:

$T = T_c + T_r$

Now, let us consider what happens after the collision. In the center of mass frame (which is special, as we now know) the initial total momentum is zero ($m \vec{r} - m \vec{r} = \vec{0}$) So, the final momentum must be zero. Following the same transformation reasoning, the final velocities in the original frame can be expressed as:

$\vec{v_1'} = \vec{V} + \vec{r'}$

$\vec{v_2'} = \vec{V} - \vec{r'}$

Here, $\vec{r'}$ is the relative velocity in the final state (after the collision). With pretty much the same derivation, the final kinetic energy $T'$ can be expressed as (obviously, in the original frame):

$T' = T_c + T_r'$

$T_c = \frac{1}{2}m V^2 + \frac{1}{2}m V^2$ (exactly the same as before)

$T_r' = \frac{1}{2}m r'^2 + \frac{1}{2}m r'^2$

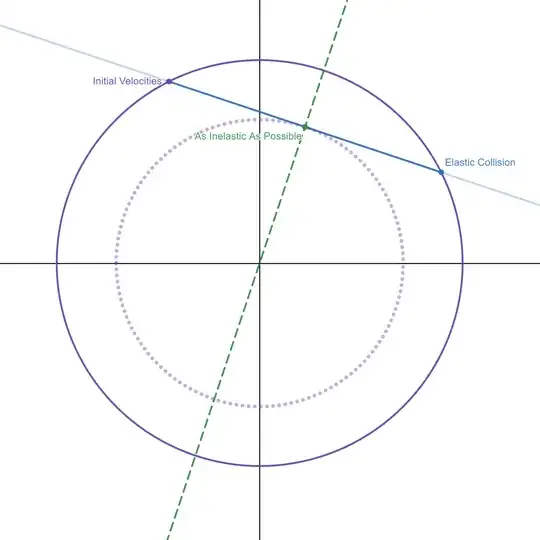
So, the kinetic energy due to the motion of the center of mass does not change. That is essentially due to conservation of momentum. What can change is the motion relative to the center of mass, which depends on the details (and elasticity) of the collision.

For a perfectly elastic collision,

$|\vec{r}| = |\vec{r'}|$

In general, due to conservation of energy:

$|\vec{r'}| \leq |\vec{r}|$

(Unless some energy is released from another source, but that is not what we are considering here.)

For a perfectly inelastic collision, $\vec{r'} = \vec{0}$. The kinetic energy after the collision will then just be the energy due to the motion of the center of mass - the system becomes lumped, and its "components" no longer carry any kinetic energy.

Just to re-iterate the key point: The center of mass frame is special in the sense that, the kinetic energy in any_other_reference_frame can be expressed as a sum of the kinetic energy of the center of mass in that reference frame, plus the kinetic energies of the bodies in the center of mass reference frame. So, after a collision, since you can not alter the velocity of the center of mass of a system without the action of external forces, that part of kinetic energy is fixed. What you can lose is the kinetic energy of the bodies in the system due to motion relative to the center of mass. And that happens only in the case of a perfect inelastic collision, where the bodies stick together and are motionless in the center of mass frame.

As such, that is the most kinetic energy that can be lost. QED.

Answer 2

This can easily be turned into a Calculus-$1$ constrained minimization problem.

You are wanting to minimize the total kinetic energy $$K=\frac12m_1v_1^2+\frac12m_2v_2^2$$

given the constraint from conservation of monmentum $$m_1v_1+m_2v_2=p_0$$

You can then easily show (work left to you) that $K$ is minimized under this constraint when $$v_1=v_2=\frac{p_0}{m_1+m_2}$$

i.e. when the objects are moving at the same velocity. Of course, since this happens in a perfectly inelastic collision, this type of collision minimizes kinetic energy of the system.

Answer 3

It is an important result that the kinetic energy of a system of any number of particles, is minimum in the reference frame attached to the center of mass. So, if you want to lose the maximum energy possible, you need to end up with such a final configuration in the center of mass frame, such that none of the particles is moving (This is lowest final kinetic energy you can achieve, namely, 0). The above situation is only possible, if all the particles come to rest in the center of mass frame just after the collision,in other words, all the particles "stick" to one another.

This argument is superior than the arguments provided in other answers, since this argument is valid for any number of simultaneously colliding particles.

For the common case of two particles, the kinetic energy in the center of mass frame can be written as

$$KE_{\rm COM}=\frac 1 2 \frac{m_1 m_2}{m_1+m_2} v_{\rm rel}^2$$

where $m_1$ and $m_2$ are the masses of the particles, and $v_{\rm rel}$ is the magnitude of the relative velocity of both the particles. As expected, if both the particles stop moving (become stationary, or stick after the collsion) in the center of mass frame of reference $v_{\rm rel}$ becomes zero and so does the kinetic energy. And this is the physical reason you're looking for.

Answer 4

But just because the k.e is 0 in some frame doesn't mean that it is the least possible in every other frame, does it?

I would like to stress on something important : ! Kinetic energy can never be negative

Zero is the minimum possible kinetic energy !

---

Just some context :

The centre of mass frame of reference is especially useful in studying nuclear collisions.

Just look here.

Answer 5

According to Noether's Theorem, if we make a Galilean transformation, and give a system of moving particles a total momentum of $\vec p$, then $\vec p - m_{tot}\vec v_{cm}=0 $, where $m_{tot}$ the total mass of the particles, and $\vec v_{cm}$ the velocity of the center of mass frame.
This means that, regardless of $\vec v_{cm}$, we can always transform the moving CM-frame into a CM-frame with zero velocity, in which it is obvious that after an inelastic collision the particles stick together and have zero momentum and thus zero velocity (the very definition of a non-moving CM-frame is the frame in which the total momentum remains zero before and after the collision), which means that kinetic energy has the minimum of zero Joules.

Answer 6

My question is, why, of all possible combinations of final velocities that conserve momentum, does this one lead to the greatest loss in kinetic energy?

There's a cute geometric interpretation that I want to show.

We'll consider collisions in one dimension. Let $m_1$, $m_2$ be the masses of the two objects; $v_1$, $v_2$ be the velocities.

The velocities of the two objects can be represented, through some modification, as points in a plane. Since

$$\text{KE}=\sum_{i=1}^N\frac{1}{2}m_iv_i^2$$

we might become inspired to plot our points as

$$(x, y) = (\sqrt{m_1}v_1, \sqrt{m_2}v_2)$$

Now if we consider a specific snapshot in time, the set of all points which have a constant KE is defined by a circle:

$$\text{KE}=\frac{1}{2}(x^2+y^2)$$

centered around the origin, with radius $\sqrt{2\,\text{KE}}$.

Likewise, since conservation of momentum is defined as

$$m_1v_1 + m_2v_2 = \text{const.}$$

the set of all points that have a constant momentum is defined by a line:

$$y = -\sqrt{\frac{m_1}{m_2}}(x-x_0) + y_0$$

$$\rule[0]{200pt}{0.4pt}$$

So a collision corresponds to some "jump" around the plane. Conservation of kinetic energy as a circle and conservation of momentum as a line will, in most cases, delineate one other intersection. This intersection denotes an elastic collision.

However, if kinetic energy is lost, then we are confined to a disk within the plane. If we take into consideration momentum conservation, then this just becomes a line segment.

Where on this line segment do we lose the most kinetic energy? The radius of our $\text{KE}$ circle was defined by $\sqrt{2\,\text{KE}}$, which means that we want our new point to be as close as possible to the origin.

In other words, if we drew a line from the origin to the most inelastic point, it would be perpendicular to the momentum line.

But the slope of the momentum line is already given as $-\sqrt{m_1/m_2}\,$. So the most inelastic line must have the equation

$$\begin{align*} y&=\sqrt{\frac{m_2}{m_1}}x \\ \sqrt{m_2}v_2 &= \sqrt{\frac{m_2}{m_1}}\sqrt{m_1}v_1 \\ v_2 &= v_1 \\ & \qquad \qquad \qquad \qquad \blacksquare \end{align*}$$

Note that this result is invariant of initial conditions, as expected.

$\rule[0.1pt]{300pt}{0.4pt}$

To connect this answer to the discussion on changing reference frames, note that a change in frame corresponds to translations of the origin about the $\sqrt{m_2/m_1}$ line; the line of perfect inelasticity. When the origin happens to land on the momentum line, this frame is the center-of-mass frame.

This interpretation was inspired by a youtube video by 3Blue1Brown.

Answer 7

For a perfectly inelastic collision, there is a reference frame (the center of momentum frame) in which the final state has zero kinetic energy, and zero is the absolute minimum.

Answer 8

If I understand your question correctly, then the answer would simply be realizing what the C.O.M frame does to a two-body problem. If you recall a two body problem can be converted into a one-body problem in the C.O.M frame. This means that equations of motion for the now new one body are equivalent to the original scenario.

Since Kinetic Energy(at least classically) cannot be negative , minimum corresponds to it being zero (with max loss) , hence it cannot be any lower for any other frame.

Now what I mean by this is. Let's take this inelastic collision from some other frame where the K.E has some value. If this collision instead were elastic , computing K.E from the chosen frame$ will give value greater than that for the previous case. So basically getting the most minimum value possible (=0) for K.E. from C.O.M frame implies that if you had chosen any other frame where K.E. was not zero , an elastic collision observed from this frame will give a greater K.E and hence and lesser loss. The key is that for comparing elastic and inelastic collision you have to stick to one frame whatever that maybe.

Answer 9

If you don't want calculus and need a physical interpretation, here's one:-

Meaning of inelastic collision is some energy of collision transforms into potential energy, either by changing shape or heat or sound etc.

So, in a perfect inelastic collision, the maximum amount of energy is converted into potential energy. And by conservation of energy, maximum kinetic energy is lost. (Considering environment to be a part of system.)

Answer 10

But just because the KE is 0 in some frame doesn't mean that it is the least possible in every other frame, does it?

Yes, it does. Given two states with the same momentum, the question of which one has most kinetic energy is the same in all reference frames. Remember that while "how much" of something we measure can be different in different reference frames, broader questions of what happens are the same. If in the reference frame of the center of mass, kinetic energy is converted to heat energy, then every reference frame will see kinetic energy being converted to heat. They will disagree about how much energy is converted, but not that some is (and that that amount is positive).

This rule that ordering of kinetic energy is invariant under boosts doesn't apply if momentum isn't constant. If momentum changes, then that means that it's experiencing a force between it and another object, which means that there can be a flow of energy between it and the other object, and different frames of references can disagree as to whether it is gaining or losing energy to that other object.

Kinetic energy being converted to heat is objectively physical in a way that gaining or losing energy isn't. If you see a thermometer changing what temperature it's displaying, then you know that the temperature is increasing. It being in a different frame of reference frame means that the "actual" temperature is different from what the thermometer reads, but the sign of the change is the same. If it's a mercury thermometer, for example, everyone will agree that the mercury expanded, but they will disagree as to the volume of the expansion (because it's going to be affected by Lorentz contraction).

Answer 11

Here is a calculus style argument without an appeal to the center of mass frame. I'll assume 1 dimension and 2 objects with mass $m_1$ and $m_2$. To eliminate some subscripts, the velocities ($v_1$ and $v_2$) and kinetic energy ($T$) are after the collision. The kinetic energy of the system after the collision is:

$$T = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2$$

We can use the first derivative test to find the velocity that minimizes the kinetic energy. I'll do it for the first object, but you could choose the second.

$$\frac{\partial T}{\partial v_1} = m_1 v_1 + m_2 v_2 \frac{\partial v_2}{\partial v_1}$$

The chain rule term ($\frac{\partial v_2}{\partial v_1}$) means you need to know how the two final velocities relate to each other. This is answered by conservation of momentum. Since the total momentum ($p$) of the system has a unique and unchanging value, the two final velocities are related. It is convenient to take a derivative with respect to the first particle's final velocity.

$$ p = m_1 v_1 + m_2 v_2$$

$$\frac{\partial p}{\partial v_1} = m_1 + m_2 \frac{\partial v_2}{\partial v_1}$$

Since the momentum is conserved (i.e. its value is a constant), any derivative acting on it will give zero.

$$0 = m_1 + m_2 \frac{\partial v_2}{\partial v_1}$$

Therefore: $$\frac{\partial v_2}{\partial v_1} = - \frac{m_1}{m_2}.$$

Put this back into the derivative of kinetic energy equation:

$$\frac{\partial T}{\partial v_1} = m_1 v_1 + m_2 v_2 \left(-\frac{m_1}{m_2}\right)$$

$$\frac{\partial T}{\partial v_1} = m_1 v_1 - m_1 v_2$$

You can find the condition on $v_1$ to minimize the kinetic energy by setting $\dfrac{\partial T}{\partial v_1} = 0 = m_1 v_1 - m_1 v_2$, therefore $v_1 = v_2$ is the condition necessary to minimize the kinetic energy.

So to minimize the kinetic energy after the collision, the two objects leave the collision moving in the same direction and at the same speed (i.e. they are effectively if not literally joined).

To be careful, the first derivate merely shows that the kinetic energy is at a minimum, maximum, or inflection point. To distinguish, use the second derivative test.

$$\frac{\partial T}{\partial v_1} = m_1 v_1 - m_1 v_2$$

$$\frac{\partial^2 T}{\partial v_1^2} = m_1 - m_1 \left(\frac{\partial v_2}{\partial v_1}\right),$$ again use how the two velocities are related.

$$\frac{\partial^2 T}{\partial v_1^2} = m_1 - m_1 \left(-\frac{m_1}{m_2}\right)$$

$$\frac{\partial^2 T}{\partial v_1^2} = m_1 + \frac{m_1^2}{m_2}$$

Since masses are positive, $\dfrac{\partial^2 T}{\partial v_1^2} > 0$, so the curvature is positive, so the kinetic energy was minimized.