How does quantum field theory connect to dynamics of particles?

Question

So, in quantum field theory, how can one describe dynamics of a system of particles? According to what equation does this system evolve? Can one see how this system is moving through space? Is this described by equation of motion for a quantum field or by dynamics of many particle states? In QFT books there is much talk about transitions between many particle states but never have i seen well explained dynamics and how to connect abstract math to a real world motion and dynamics similar to QM.

Answer 1

QFT (quantum field theory) describes particles as excited states (quanta) of their underlying fields, which are regarded as more fundamental than the particles. Interactions between particles are described by interaction terms in the Lagrangian involving their corresponding fields.

The dynamics is given by the Euler–Lagrange equation applied to the action $S = \int d^4x \mathcal L$, where $\mathcal L = \mathcal L(\phi, \partial_\mu \phi)$ is the Lagrangian density and $\phi$ here for simplification represents all the various fields.

The Euler–Lagrange equation is
$\frac{\partial \mathcal L}{\partial \phi} - \partial_\mu \frac{\partial \mathcal L}{\partial (\partial_\mu \phi)} = 0$

In QFT the fields $\phi$ are promoted to operators and acting on the vacuum state can create or destroy particles. The operator $\phi (x)$ creates a particle at $x$. A realistic description of a particle, i.e. an object localized in a limited region of spacetime, is given via a Gaussian packet. The dynamics of the particles follows from the dynamics of the fields.

Answer 2

So, in quantum field theory, how can one describe dynamics of a system of particles?

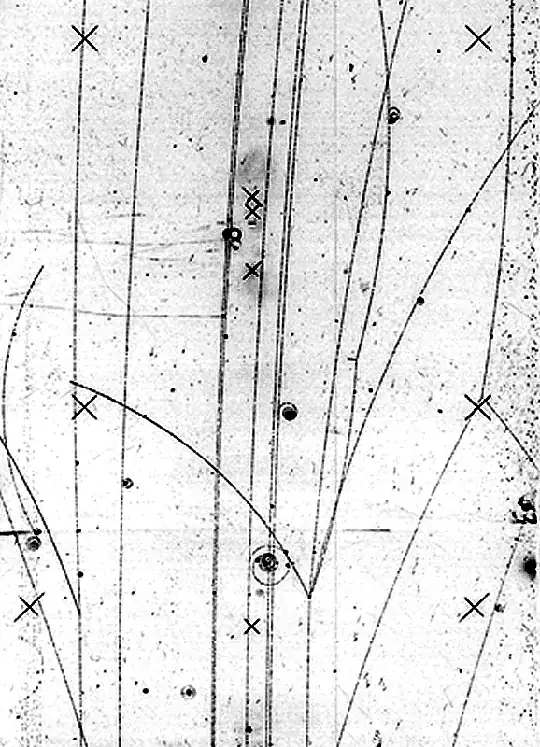
In general the dynamics are at a $(Δx, Δy ,Δz, Δt)$ region of the four dimensional space , where the interaction described by quantum field theory takes place, the "event", at its center of mass, the system of particles described by Feynman diagrams. When dimensions become macroscopic, there are no interactions to describe, just particle tracks in fourspace.

According to what equation does this system evolve? Can one see how this system is moving through space?

According to classical mechanics.

In this single event picture we see in the recording of a bubble chamber a system of particles coming out of a point as far as our accuracy of measurement goes. The tracks leaving the point are treated with classical mechanics equations. Accumulating such events gives the crossection, calculated using the QFT feynman diagrams.

If one wanted to use QFT to describe the tracks of the leaving particles , not very smart, one would start with wave packets of creation and annihilation operators running across the track.

" but never have i seen well explained dynamics and how to connect abstract math to a real world motion and dynamics similar to QM."

The solutions of the basic QM equations do not describe classical motion of particles in space. Just interaction of particles with potentials.

Answer 3

In QFT all processes are considered to be happening inside the "black boxes", and the theory is aiming at predicting the outputs of the black box from given inputs.

Creation and annihilation operators (and their commutation relations) are used to get rid of input particles and to transform them into ouput particles. We just annihilate inputs and create outputs according to some rules. Black boxes can be visualized as vertices of Feynman diagrams.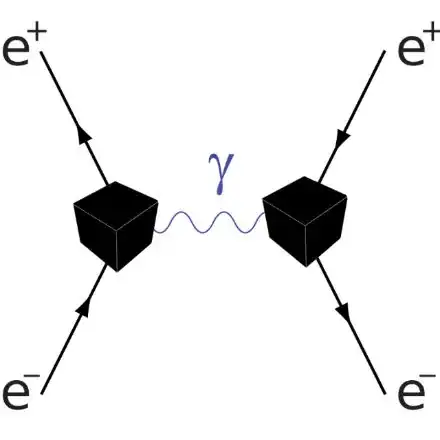

The dynamics study how a physical system might develop or alter over time. In QFT this is achieved by the series of the transformations of inputs to outputs inside the "black boxes".