How can one mathematically demonstrate that angular displacement is not a vector and is not commutative?
1 Answers
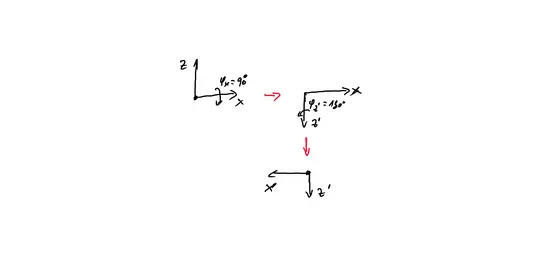
look at this figure.
you want to bring the (x,z) axes to (x',z') axes you can do it by applying two rotations. first rotation $\frac \pi 2$ about the x axes and the second rotation $\pi$ about the z' axes. each rotation ,can describe mathematically by a $3\times 3$ Matrix.
First Rotation Matrix
$$S_x=S_x(\frac \pi 2)$$
second Rotation Matrix
$$S_{z'}=S_{z'}(\pi)$$
thus: $(x,y)\mapsto (x',z')$ by multiply the rotation matrices $$S=S_x(\frac \pi 2)\,S_{z'}(\pi)$$
because matrix multiplication is not commutative, thus the angles are not vectors, but also you can't create the matrix S by addition the angles.
Edit:
$$S_x(\frac \pi 2)=\left[ \begin {array}{ccc} 1&0&0\\ 0&0&-1 \\ 0&1&0\end {array} \right] $$
$$S_{z'}(\pi)=\left[ \begin {array}{ccc} -1&0&0\\ 0&-1&0 \\ 0&0&1\end {array} \right] $$
$$S=S_x\,S_{z'}=\left[ \begin {array}{ccc} -1&0&0\\ 0&0&-1 \\ 0&-1&0\end {array} \right] $$
and
$$S\,\begin{bmatrix} x \\ 0 \\ z \\ \end{bmatrix}= \begin{bmatrix} -x \\ 0 \\ -z \\ \end{bmatrix}~\surd$$
- 13,829