Time dilation in Einstein's train

Question

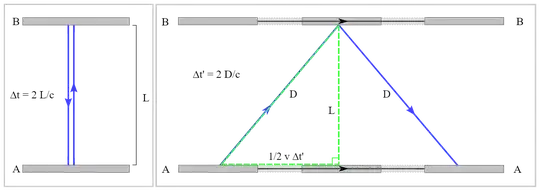
Wikipedia states that

a clock that is moving relative to [observer] will be measured to tick slower than a clock that is at rest in their frame of reference

and they explain it using two pictures:

Left: Observer at rest measures time 2L/c between co-local events of light signal generation at A and arrival at A.

Right: Events according to an observer moving to the left of the setup: bottom mirror A when signal is generated at time t'=0, top mirror B when signal gets reflected at time t'=D/c, bottom mirror A when signal returns at time t'=2D/c

Let's assume that the second picture is a train going from left to right. Signal travels perpendicular (90°) to the motion of the train.

Now instead of positioning the mirrors on the floor and ceiling, what if I put mirror A to the back and mirror B to the front of the train (still facing each other). The signal now runs parallel (0° or 180°) to the motion of the train. It travels long way from A to B and short way back to A, effectively cancelling the time dilation effect at the end of the A-B-A trip.

It seems to me that I can tweak the angle between perpendicular (90°) and parallel (0° or 180°) to increase or decrease the time dilation effect.

Now if above is true does it mean that, contrary to what Wiki says, it is possible to position the clock in a way that it will be measured to tick at the same rate (not slower) than a clock that is at rest in observer's frame of reference?

Answer 1

If you have a horizontal signal, you will get that $\Delta t=2L/c$, and $\Delta t'=2L'/c=2L/c\gamma=\Delta t'/\gamma$. The reason is that now you have a component of the light moving in the same direction than S', and so length contraction plays a role.

However, to use such clock you need to know and correct for length contraction. In the case the light goes perpendicular to the motion you do not need to consider this effect.

Answer 2

It travels long way from A to B and short way back to A, effectively cancelling the time dilation effect at the end of the A-B-A trip.

If we could write the longer path as $L'+\Delta L'$, and the shorter one as $L'-\Delta L'$, and if there was not anything such as length contraction ($L=L'$) , your claim would be correct and the clock would be measured to tick at the same rate.

However, calculations show that the longer path complies with $L/(1-\sqrt{\beta})$, and the shorter one does with $L/(1+\sqrt{\beta})$, where $\sqrt{\beta}=v/c$. On the other hand, the Lorentz contraction implies $L=L'\sqrt{1-\beta^2}$. These mean that the shorter and longer paths do not compensate for each other to maintain the proper time measured in the clock's rest frame.