5

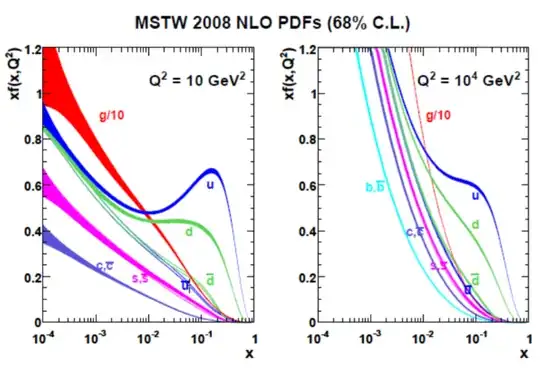
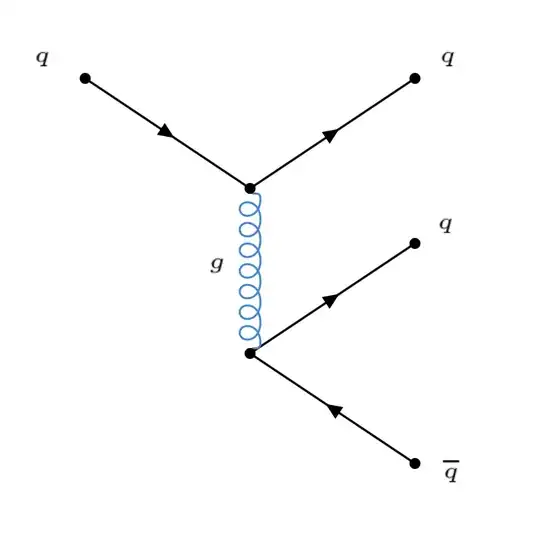
In electron proton deep inelastic scatterings, the sea quarks or gluon PDFs are only dominant at low value of $x$. Thomson explained this in his book Modern Particle Physics (see page 194) by arguing

...in reality the proton is a dynamic system where the strongly interacting quarks are constantly exchanging virtual gluons that can fluctuate into virtual $q\bar{q}$ pairs through [strong] processes...Because gluons with large momenta are suppressed by the $1/q^2$ gluon propagator, this sea of virtual quarks and antiquarks tend to be produced at low values of x.

I am not able to see what this has to do with the value of $x$. Does this mean when $x$ decreases, the four momentum $q$ of the gluon also decreases? If so, why is it the case?

DavidH
  • 3,275
Hector
  • 83

3 Answers3

2

So the Parton distribution functions are "essentially" the probability distributions (very suspicious how both are called pdf) of a probe particle to interact with a component inside your hadron. They depend both on the momentum at which we probe $Q^2$ and the fraction of momentum carried by said parton, the Bjorken x. They are mostly known through experiment as we have a poor understanding of non-perturbative QCD and the DGLAP equation governs the evolution ( and I'm sure more recent development I am not aware of).

pdf

So let's look at the first graph, this is the PDF of (you guess it) a proton. We see this because the up quarks peaks at around $\sim 0.2$ momentum fraction and has twice as much weight as the down quark. On the other hand, the gluon distribution kinda blows-up as you get close to $0$ momentum fraction (the graph has the gluon pdf divided by 10 near in mind!).
This actually makes sense because they are massless particles and it is much more easy to put a massless particle on shell than a massive particle. That's why massless particles tend to create particle showers in scattering experiments (EM showers and jets). Another way to think about this is that this is an IR (or soft) process and there exists a whole technology to resum these.
Same story for the sea quarks, they are quantum fluctuations away from "a hadron has 3 more quarks than anti-quarks", so their pdf is suppressed as well.

I hope I've given enough of an answer here, but really, you just need to be able to read these graphs and it will all make sense eventually. We could also discuss the relationship with $Q^2$ in the comments, there is also a nice physical interpretation there.

thecakeisLie
  • 196
1

My QCD knowledge is very limited - I haven't learnt it anywhere else other than in some qualitative discussion in Thomson's particle physics textbook. So I was only seeking a qualitative answer to aid my understanding in PDFs.

Thanks to @anna_v 's answer I realised I hadn't gone through Thomson's own slides of the chapter and the answer lies there all along.

If we consider the following quark-antiquark pair production strong process in an electron proton deep inelastic scattering experiment

Since the gluon is suppressed by the $1/q^2$ gluon propagator:

$$-i \frac{g_{\mu\nu}}{q^2} \delta^{ab}$$

the pair production is more likely to happen at low value of $q$. Now it is easy to see that the momentum of the pair produced sea quarks is just the momentum of the virtual gluon, so a low $q$ indeed indicates a low momentum fraction $x$ of the interacting sea quarks.

The slide can be found here under chapter 8 or in the first link in @anna_v 's answer.

Hector
  • 83
0

I copy these definitions of the scattering variables"

inelscat

I am not able to see what this has to do with the value of x. Does this mean when x decreases, the four momentum q of the gluon also decreases? If so, why is it the case?

The definition of x is dependent on the four momentum carried by the propagator, in the diagram small $q$ vector , which is connected with $Q$ . This should clear for you that the larger $Q$ by the four vector dot product of $q$ with itself. From the definition, large $x$ mean large $Q$ So from the definition the larger the momentum transfers to the gluon are suppressed.

This explains the gluon propagator statement you quote, but you should read the link to see how the parton distributions are found:

Ultimately the parton distribution functions are obtained from a fit to all experimental data including neutrino scattering

In this link , parton distribution functions are discussed, but as the other answer states, it is not a simple mathematically project.

anna v
  • 236,935