Why not calculate it?
Consider a string of length $L$, with its ends fixed at $x=0$ and $x = L$. Let's assume for convenience that at time $t=0$ the string is "plucked" at $x = L/2$, so that the string displacement relative to its equilibrium position is given by
$$f(x)=A\left(1 - \left|\frac {2x} L-1\right|\right).$$
The standing wave solutions to the wave equation obeying the boundary conditions are
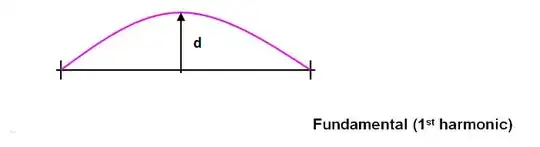
$$\psi_n(x)=\sin\frac{n\pi x}{L} $$
where $n\ge1$ is the harmonic number, with $n=1$ corresponding to the fundamental, $n=2$ to the second harmonic and so on.
It can be shown that $\psi_n$ are orthogonal, that is,
$$\int\limits_{0}^{L}\psi_m(x)\psi_n(x)dx=\frac{L}{2}\delta_{mn}$$
where $\delta_{mn}$ is the Kronecker delta. We can express the initial displacement as a linear combination of the harmonics (a Fourier series):
$$f(x)=\sum\limits_{m=1}^\infty a_m\psi_m(x).$$
Multiplying by $\psi_n$, integrating and using the orthogonality relation yields
$$a_n = \frac{2}{L}\int\limits_{0}^{L}f(x)\psi_n(x)dx =
\begin{cases}
\displaystyle (-1)^{\frac12 (n-1)}~\frac{8A}{\pi^2n^2}, & n\text{ is odd} \\[1ex]
\displaystyle 0, & n\text{ is even} \\[1ex]
\end{cases} \tag{1}\label{1}$$
so the amplitude of the harmonics decreases in magnitude as $1/n^2$. Note that plucking the string in the middle excites only the odd harmonics, so the coefficients of the even harmonics are zero. On an instrument, this results in a very distinct sound.
You find that if you pluck the string closer to the ends, the amplitude of the harmonics goes down slower, i.e. there are more "overtones". Specifically, if the string is plucked a distance $\ell$ from one of the ends, the amplitudes are
$$ b_n = \frac{2AL^2}{\pi^2\ell(L-\ell)n^2}\sin\frac{n\pi\ell}{L}\tag{2}\label{2}$$
where the sine factor accounts for the slower decay of $b_n$ when $\ell$ is small. $\eqref{2}$ is more general than $\eqref{1}$ as it is also valid when the string is not plucked in the middle, and is also consistent with how a guitar string is normally picked.
As for the energy distribution, the energy in the $n$'th harmonic is
$$ E_n = \frac{1}{4}M\omega_n^2b_n^2 = \frac{1}{4}M\omega_1^2n^2b_n^2$$
where $M$ is the total mass of the string and $\omega_n=n\omega_1$ is the angular frequency of the $n$'th harmonic. If $b_n$ decays roughly as $1/n^2$ asymptotically, so does $E_n$.