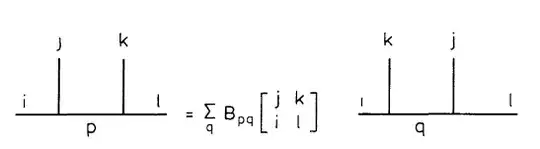Moore and Seiberg (1989) prove that rational CFTs are classified by the braiding matrices $$ B\begin{bmatrix}j_1&j_2\\i&k \end{bmatrix}\colon \bigoplus_p V_{j_1p}^i\otimes V_{j_2k}^p\to V_{j_2q}^i\otimes V_{j_1k}^q $$ which implement the duality transformations between different blocks
I am looking for the values of these matrices for WZW models. I know the answer for rational tori, $Spin(n)_1$, $SU(2)_k$ and $Spin(2n+1)_2$ (and some specific $SU(3)$ groups). Are there any other affine algebras for which these matrices are known?
In the condensed-matter literature is more common to refer to these matrices as the $F$-symbols. They implement changes of bases in anyon models. From the Chern-Simons point of view they can also be understood as the expectation value of a link in the shape of a tetrahedron, where $i,k,j,\dots$ label the different Wilson lines.
I also asked this question on mathoverflow https://mathoverflow.net/q/346017/, where I got the answer for $Spin(2n+1)_2$. I am hoping physicists know more examples, hopefully one in $SU(N)_k$ for higher $N,k$.