Is there a smooth transition from inverse quadratic gravity to linear gravity?

Question

I can't remember exactly what it was, but I remember going through a problem in physics related to gravity on and inside a sphere, and found that inside, gravity acts linearly as a result of some triple integral cancellation with an assumption on uniform density.

Suppose Earth itself was a perfect sphere and you could pass through it. Does gravity actually spontaneously transition from inverse quadratically to linearly? Would it really be some magic spontaneous switch in forces? Or is there something in the math that can explain a gradual transition from a quadratic factor to a linear factor?

Answer 1

Note: Throughout the answer, I am treating the scenario from the point of view of Newtonian gravity.

Uniform solid sphere

The force function of a uniform sphere is continuous. Thus, the force never changes abruptly. Below is the graph between gravity and the distance from the sphere's center:

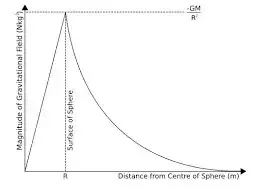
^{Image source}

As you can see, the function is a continuous one, and doesn't change it's value suddenly when you cross the surface.

Uniform spherical shell

However, in case of a uniform spherical shell, you will get to see a discontinuous force vs distance graph, something like this:

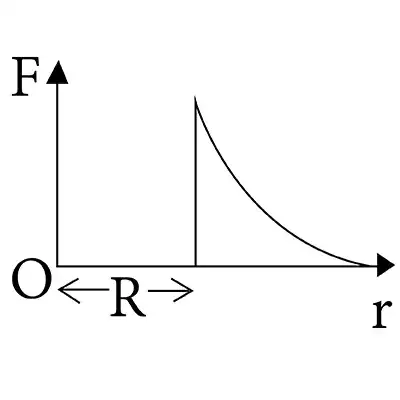
Image source

Here, the value of gravitational field/force inside the shell is zero, whereas just outside the shell, it's non-zero. This results in an abrupt change in force.

Physical feasibility

This discontinuity of a vector field is not at all unphysical or infeasible. There's nothing wrong to have an abrupt change in a force field. However, if a field has a potential associated to it (in other words, if the field is conservative), then the potential must be continuous. Because a conservative field is defined as the negative of the gradient of potential, and the gradient of the potential cannot be defined if the gradient is discontinuous. So, for a field to exist everywhere, it's potential must be continuous. The field doesn't need to satisfy continuity.

Answer 2

For a spherical body of mass $M$ and radius $R$, assuming the density is constant you can calculate the gravitational field strength at any distance $r$ from the centre of the body using Gauss's law. If you work through the algebra (which is a good exercise) you'll eventually find

$$g = \begin{cases} -\frac{MGr}{R^3}, &\qquad r \le R, \\ -\frac{GM}{r^2}, &\qquad r > R. \end{cases}$$

If you look at both expressions for $r = R$ you'll see that they agree. This means that the gravitational potential is continuous at $r = R$. If you take the first derivative with respect to $r$ of both expressions, however, you'll find that they are not the same. This means that the potential is not smooth in the mathematical sense of a smooth function.