This is kind of a weird one, so let's follow the logic step by step:
First of all, you're right that $\vec{F}\cdot\mathrm{d}\vec{r}$ should be positive. It has to be, because as you noticed, the force is always acting in the same direction as the path of integration, so each infinitesimal contribution to the integral is going to be positive. If you expressed it as a Riemann sum, you'd be summing up a bunch of positive quantities.
Given that $\vec{F}\cdot\mathrm{d}\vec{r} > 0$, and $\vec{F}$ obviously points in the negative $\hat{r}$ direction, it must also be the case that $\mathrm{d}\vec{r}$ points in the negative $\hat{r}$ direction. You might say
$$\mathrm{d}\vec{r} = -\lvert\mathrm{d}r\rvert\hat{r}$$
But here's the tricky part. That last equation actually involves two different variables. The $\mathrm{d}\vec{r}$ on the left side is a differential that represents an infinitesimal progression along the path of integration (what might be otherwise denoted $\mathrm{d}\vec{\ell}$ or $\mathrm{d}\vec{s}$), while the $r$ on the right side is a coordinate which measures distance from the origin (what might otherwise be denoted $\rho$, or $x$ if you're integrating along the $x$ axis, or so on).
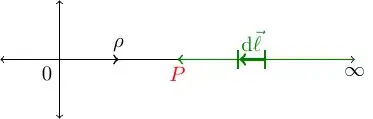
So to avoid confusion, you might want to write
$$\mathrm{d}\vec{\ell} = -\lvert\mathrm{d}\rho\rvert\hat{\rho}$$
Now, as you step along the line of integration from $\infty$ towards $P$, $\rho$ decreases. So if you're going to do a change of variables to replace $\mathrm{d}\vec{\ell}$ with its expression in terms of $\rho$, you're going to need $\mathrm{d}\rho < 0$, which in turn means that $\mathrm{d}\vec{\ell} = \mathrm{d}\rho\,\hat{\rho}$. Therefore,
$$\int_{\infty}^{P}\vec{F}\cdot\mathrm{d}\vec{\ell} = \int_{\rho=\infty}^{\rho=r_P}\biggl(-G\frac{Mm}{\rho^2}\hat{\rho}\biggr)\cdot(\mathrm{d}\rho\,\hat{\rho})$$
The difference with what you were trying to do was that you assumed $\mathrm{d}r$ (non-vector, after the dot product) would be positive. That $\mathrm{d}r$ actually corresponds to $\mathrm{d}\rho$, and is negative. Roughly speaking, you implicitly did a change of variables from $\ell$ to $\rho$, which introduces a sign change, but it was hidden from you because you used the same letter ($r$) for both variables.
A precise formulation
Here's a fully precise way to do this: take the definition of work as a line integral of the force vector field,
$$W = \int_{0}^{1} \vec{F}\bigl(\vec{r}(s)\bigr)\cdot\underbrace{\vec{r}'(s)\,\mathrm{d}s}_{\mathrm{d}\vec{\ell}}$$
In this definition, $s$ is a parameter of the path of integration, which ranges from $0$ at the beginning of the path to $1$ at the end. So in your case, $s = 0$ at infinity and $s = 1$ at $P$. One possible realization of this, if you assume that $P$ is a point on the $x$ axis, is
$$\vec{r}(s) = \biggl(\frac{r_P}{s}, 0, 0\biggr)$$
Using the above realization, we have
$$\begin{align}
\vec{r}'(s) &= \biggl(\underbrace{-\frac{r_P}{s^2}}_{\mathrm{d}\rho/\mathrm{d}s}, 0, 0\biggr) = -\frac{r_P}{s^2}\hat{x} &
\vec{F}\bigl(\vec{r}(s)\bigr) &= -G\frac{Mm}{(r_P/s)^2}\hat{x}
\end{align}$$
Note that this makes the direction of $\vec{F}$ radially inward, as it should be, at all points along the line of integration.
Plugging these into the formula for work, we get
$$W = \int_{0}^{1} \biggl(-G\frac{Mm}{(r_P/s)^2}\hat{x}\biggr)\cdot\biggl(-\frac{r_P}{s^2}\hat{x}\biggr)\,\mathrm{d}s = G\frac{Mm}{r_P}\int_0^1\mathrm{d}s = G\frac{Mm}{r_P}$$
"Guide questions" for self-study
In case you'd like to ponder this more deeply, here are some "guide questions" to think about:
- Convince yourself that, as $s$ ranges from $0$ to $1$, $\vec{r}(s)$ traces out the path on which you want to integrate.
- How does each component of $\vec{r}$ vary as $s$ changes from $0$ to $1$? Larger, smaller, or the same? Try making a drawing that shows it.
- What are some other possible formulas for $\vec{r}(s)$ that would describe the same path?
- What are some other paths, and the formulas that describe them, which would also be suitable for this physical situation? (E.g. if you don't assume $P$ is on the $x$ axis)
- What is the sign of the x-component of $\vec{r}'(s)$?
- Is that consistent with how your position changes as you move along the integration path?
A comparison
It's been pointed out that an answer to another, similar question says that $\mathrm{d}\vec{r}$ is not a vector directed along the path. After looking into it, I believe that's not correct, for a similar reason to what you did here: that answer uses the definition
$$\mathrm{d}\vec{r} = \mathrm{d}r\,\hat{r} + r\,\mathrm{d}\theta\,\hat{\theta} + r\sin\theta\,\mathrm{d}\phi\,\hat{\phi}$$
but that expression is for the differential of the coordinate vector (of which my $\mathrm{d}\rho\,\hat{\rho}$ is the radial part). $\mathrm{d}\vec{\ell}$ is a different entity, which is directed along the integration path.
