What force accelerates a liquid moving in a narrowing pipe?

Question

Say there is a liquid which behaves like an incompressible fluid and is flowing steadily through a pipe which is moving from a cross section of area $A_1$ to the cross section of area $A_2$, where $A_2$ is less than $A_1$. As per the continuity equation, $v_2>v_1$ and so the liquid seems to be accelerating. What force is causing this acceleration?

Answer 1

You are right. From continuity of the incompressible fluid you have $$A_1 v_1 = A_2 v_2.$$ So obviously the velocity is changing. Thus the fluid is accelerated, and therefore there must be a force causing this acceleration. In this case the force comes from the pressure difference between the wide and the narrow part of the pipe.

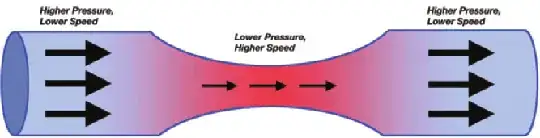
_{(image from ResearchGate - Diagram of the Bernoulli principle)}

This can be described by Bernoulli's equation ($p$ is pressure, $\rho$ is density) $$\frac{1}{2}\rho v_1^2 + p_1 = \frac{1}{2}\rho v_2^2 + p_2$$

Answer 2

There is more mass per area behind than ahead of the constriction so since ppressure is force divided by area there develops a pressure difference

Answer 3

The simple answer is pressure.

As you state, from the continuity equation you can see that the velocity $v_2>v_1$. The next step is a momentum balance (like any balance in fluid dynamics: $\frac{d}{dt}=in-out+production$). The momentum flowing into the system is smaller than the momentum flowing out of the system ($\rho A_1 v_1^2 < \rho A_2 v_2^2 = \rho A_1 v_1^2 \frac{A_1}{A_2}$, $\frac{A_1}{A_2}>1$).

The actual force is not the pressure itself, but the pressure difference, or, actually, the difference in force, because on the left the force is $p_1 A_1$ and on the right $p_2 A_2$.

From another conceptual point. Suppose you have a garden hose. Than you have a fixed pressure drop. Now, if you squeeze it, you create a contraction. Part of the pressure drop is now needed to accelerate the fluid at the exit. The overall flowrate decreases, because you also need pressure to overcome frictional forces.

Answer 4

It's simple.

Connect the garden hose to the bottom of the large beaker, keeping the height of the water surface in the beaker constant, with a speed of v1 and a pressure of P1.

Reducing the cross-sectional area of the outlet of the garden hose obstructs the flow of water, causing congestion and resulting in less outflow and more inflow. So, the pressure will increase until it reaches P2, where the inflow and outflow are equal and the pressure no longer increases.

So, the pressure increases due to overcrowding; Due to congestion, the speed has decreased to V2.

However, due to the increase in pressure, the velocity increases to V3 at the contracted outlet. Obviously, V3 is greater than V2 and also greater than V1.

That's how high pressure comes about, and V3 comes about because of high pressure.