If I hold a ladder at an incline to a frictionless surface and then release it, will it slide?

Question

I am trying to determine whether the ground exerts a horizontal frictional force On the ladder (in addition to the normal contact force) when the surface is not frictionless and came up with the above thought experiment. If there exists such a force, then in its absence, the ladder should also slide in addition to falling.

If such a force does exist, what is causing it? I understand that friction on the ladder is the horizontal component of the reaction force to that exerted by the ladder in the ground , but there is only a vertical gravitational force on the ladder pushing it vertically into the ground, so shouldnt the reaction force be vertically upward only?

I have a feeling that this has something to do with moment, of which i have only the basic knowledge

Answer 1

I am trying to determine whether the ground exerts a horizontal frictional force On the ladder (in addition to the normal contact force) when the surface is not frictionless and came up with the above thought experiment. If there exists such a force, then in its absence, the ladder should also slide in addition to falling.

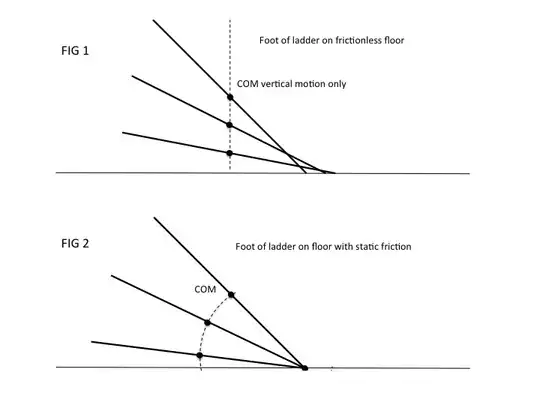
You are correct that, in the absence of friction on the ground, the ladder will slide on the ground in addition to falling. Since there would be no external horizontal forces acting upon the ladder, the center of mass (COM) can only have vertical motion. For the motion to be strictly vertical, the foot of the ladder has to slide. See Fig 1 below.

But we also know that if friction is present it will oppose the relative motion between the foot of the ladder and the ground. Friction will either prevent relative motion between the surfaces (static friction), or act in opposition to the sliding motion (kinetic friction). If the maximum possible static friction force is not exceeded, horizontal motion (sliding) will be prevented and the motion of the COM will follow a circular path, as shown in Fig 2 below.

I understand that friction on the ladder is the horizontal component of the reaction force to that exerted by the ladder in the ground, but there is only a vertical gravitational force on the ladder pushing it vertically into the ground, so shouldn’t the reaction force be vertically upward only?

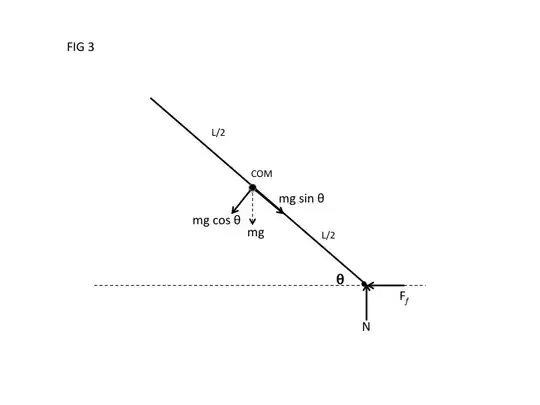
Although the gravitational force acts vertically on the COM, the gravitational force can be resolved into components acting parallel and perpendicular to the ladder at the COM. See Fig 3 below. The component that acts parallel to and down the ladder can be resolved into normal and horizontal (friction) reaction forces.

By the way I came across the following answer by @ja72 to a similar question: Motion of the center of mass of a falling rod. Note the graphic provided by ja72.

Hope this helps.

Answer 2

Yes, it has to do with moments.

For equilibrium the sum of the forces has to be zero and the sum of the moments about any point must be zero.

Assume the ladder is leaning against a frictionless wall at the left and on a floor with friction at the right. See the free body diagram of the ladder below. Take the point of contact with the floor (point B). For simplicity assume the total gravitational force on the ladder of W equals the weight of the ladder plus load acts at the center of the ladder.The gravitational force W on the ladder causes a counterclockwise moment about the floor at A. Assuming a frictionless wall a normal reaction force $R_W$ horizontal to the wall at A is required to provide an equal clockwise moment about the floor so that the sum of the moments about B is zero. Then, in order for the sum of the horizontal forces to be zero, you need a horizontal static friction force $F_f$ equal to the horizontal reaction force of the wall $R_W$.

Hope this helps.

Answer 3

I have considered the vertical wall as frictionless for the sake of simplicity.

If we consider this ladder in equilibrium then the vertical wall exerts a reaction force $\vec{N_{1}}$ whereas the floor exerts a rection force $\vec{N_{2}}$.Earth exerts weight $m\vec{g}$ on the ladder on its centre of gravity.

If this ladder is in translation equilibrium then there must be a force directed opposite to $\vec{N_{1}}$ that's why floor must exert a horizontal force $\vec{f}$ on the ladder which we call as friction.

In terms of rotational equilibrium,let's consider the net torque about the centre of ladder then $N_{1}$ provides a torque directed outside the plane of screen whereas $N_{2}$ also provides a torque outside the plane then there must be a force which provides torque directed inside the plane of screen.This force is friction which is exerted by the floor on the wall.

Answer 4

Frictionless surface can produce only reaction force in the direction perpendicular to the surface in the point of contact. Any tangential force produced by the surface is by definition force of friction. No force of friction can be perpendicular to the surface.

So the ground exerts only horizontal frictional force. The point of contact of ladder should be sticked to the surface, which means the net vertical force acting on the point of contact is supposed to be zero, otherwise ladder at the point of contact would jump upwards or fall under the ground. The vertical force is the force of constraint - this force is such that the point of contact remains the same - which is your requirement based on the physical situation. Because of its direction, it is called normal force.

So we fixed vertical force by our constraint that point of contact must remain at contact. The only component we are left with is horizontal component, which is by definition force of friction.