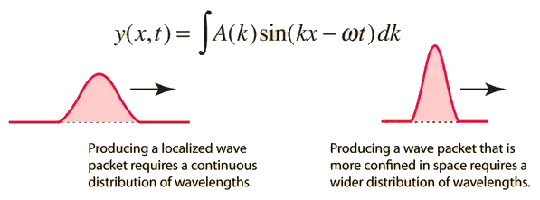Are monochromatic EM waves supposed to be sinusoidal?

Question

This question remind me of a doubt on the relation between colors and frequencies.

When we talk about a monochromatic color of a given frequency (or at least a narrow range of frequencies), it means only a generic plane wave with a narrow range of $k$:

$f(k(x - ct))$ where $\omega = kc$.

Or is this type of wave supposed to be sinusoidal as suggested by this answer?

Different musical instruments and the human voice can produce the same tune, (same frequency) but the sound is not the same. There is a difference of tone (I am not sure if that is the correct English word for the sound difference). That difference in tone is related to the wave shape in my understanding.

I wonder if it happens also with EM waves. Of course, man made radio waves can be very pure sinusoidal as mentioned here. But and about light?

Does the blue of a Yves Klein painting depends only on frequency or also on the wave shape?

Answer 1

If the wave is truly monochromatic then it will be sinusoidal. If it has a different profile then Fourier's theorem tells us that it can be built from an infinite series of (co)sine waves with increasing integer harmonics of the principle frequency (i.e. not monochromatic).

Answer 2

A plane wave is a single frequency , a sinusoidal variation in space and time by mathematical construction.

Mathematically :

the traveling wave solution to the wave equation

...

is valid for any values of the wave parameters, and since any superposition of solutions is also a solution, then one can construct a wave packet solution as a sum of traveling waves

...

It is common practice to use to represent the quantity 2π/λ by k, which is called the wave vector. For a continuous range of wave vectors k, the sum is replaced by an integral

The link goes on to describe the wavepacket solutions of wave equations.

These solutions are used to describe free particles in quantum field theory too.

In the case of light they mathematically describe the small spread in frequencies in a spectrum recorded with a crystal, or difraction grating.

Does the blue of a Yves Klein painting depends only on frequency or also on the wave shape

That is a different story and depends on perception of color, that is much more complicated than simple mathematical wave packets, as explained in the link you give and the links therein. What color the brain labels an object is dependent on the chart shown there. The reason it is complicated mathematically is because it depends on a series of biological impulses that are finally interpreted by the brain as "blue": the cones in the retina,the neurons transferring the information ....the way the brain interprets the impulses is called "color perception". One perceived color can be many disparate frequencies as seen in the chart. Wikipedia has an extensive article.

Answer 3

The electromagnetic field in absence of charges and current is described by a wave equation. The solutions of the wave equations in a general setting (without symmetry contestants and without boundary conditions) are plane waves with a fixed frequency and momentum. These are purely sinusoidal $\propto \sin(k x-\omega t)$. Similarly, sound waves are the solution of the wave equation which describe the phonon excitations in a media. Phonons are quantum of sounds, analogously to photons which are quantum of light. So, sound and light are described by very similar mathematical objects. The main difference is the speed of propagation, that is, speed of light vs speed of sound. A common and important feature of all wave equations is linear superposition. That means that if there are two solutions $\propto \sin(k x-\omega t)$ and $\propto \sin(k' x-\omega' t)$ then their superposition is also a solution of the wave equation. Now, the timbre of a musical instrument is given by the superposition of several harmonics. That means that every note of a musical instrument is not a monochromatic wave but a superposition of many frequencies, which are usually multiple of each other. This superposition changes the "shape" of the wave. The relation between the shape of the wave and its harmonics is expressed by a mathematical operation, the Fourier transform. So, a monochromatic ray of light is analogous to a very pure sine wave sound, something like the sound of a whistle or of a flute. These are described by a single sinusoidal wave. A non monochromatic ray of light is analogous to the sound of an instrument which has a more complex timbre. These are described by a superposition of sinusoidal waves. But at the end of the day, everything can be described as a superposition of pure sinusoidal waves.

Pure colors are the colors which correspond to a single frequency. Usually colors of real objects are always a superposition of several monochromatic frequencies. This is because the color of objects correspond to the complex interaction between light and matter. As a consequence, if you shine white light on a Yves Klein painting, some frequencies are absorbed, and some deflected. The blue that you see is a complex combination of the frequencies of the visible spectrum which have been reflected by the painting. However, this is not the full story, because the human eye cannot resolve all monochromatic frequencies separately, but has only 3 receptors which are sensible to a range of frequencies which are centered around blue, green, and red (if I remember correctly). The human ear is so much more sophisticated in this sense, because it is able to resolve single frequencies, also frequencies which are very close to each other.

Answer 4

To address the core misconception: Note that any plane wave in the $x$ direction can be written as $f(k(x - ct))$. This does not imply that it's monochromatic and does not in any way define $k$. With $f$ being an unspecified function, $k$ is a completely arbitrary parameter that corresponds to rescaling the argument of $f$. That is, if the plane wave was originally written as $g(x - ct)$, we can choose any value of $k$ and define $f(\phi) = g(\phi/k)$, so that $f(k(x - ct)) = g(x - ct)$.

It follows that superimposing general functions $f(k(x - ct))$ for different values of $k$ is redundant because it doesn't provide any more wave solutions than a single value of $k$.

The parameter $k$ is called the "wave number" only if $f$ is a sinusoidal function with period $2\pi$. Under this restriction, it does make sense to decompose an arbitrary plane wave into sinusoidal (monochromatic) components each with a specific $k$. We can also say that if the original plane wave is a periodic (not necessarily sinusoidal) function of $k(x - ct)$ with period $2\pi$, then the wave numbers of the nonzero sinusoidal components will be integer multiples of $k$ (harmonics).