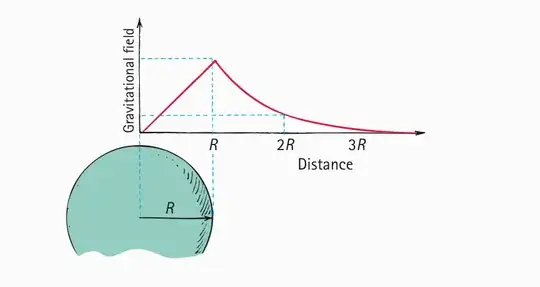
I think that, since Earth is spherical, the amount of mass in the upper half of Earth should be the same as the second half, therefore, if the strength of gravitational field increase linearly from distance 0 to R, it should also decrease at the same rate from R to 2R, however, it will never reach zero
1 Answers
The mass in the upper half is not the same as the mass in the bottom half. If we assume uniform density then the mass for the center half would be $\rho.\frac{4}{3}\pi(\frac{1}{2}R)^3=\rho.\frac{1}{6}\pi R^3$ whereas the mass of the outer half would be $\rho.\frac{4}{3}\pi[R^3-(\frac{1}{2}R)^3]=\rho.\frac{7}{6}\pi R^3$.
The field is a straight line inside the earth because the mass is increasing as we move outwards. The mass, as a function of the distance from the centre is $M(r)=\rho \frac{4}{3}\pi r^3$ (keep in mind this is valid only for r < R where R is the radius of the earth). So the field is $F(r)=\frac{GM}{r^2}=\frac{G}{r^2}\frac{4\rho \pi r^3}{3}=\frac{4GM\rho \pi}{3}r$.
Once we've reached the distance R from the centre, there is no more mass being added so the force falls as the usual $1/r^2$.
- 430