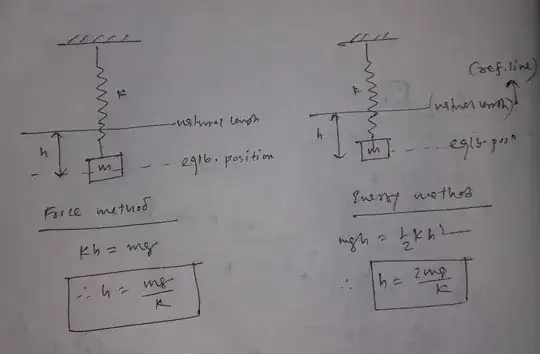
So in this example I want to find the extension produced in the spring. The two methods are given in the image.( First one is by force method and the other one is energy method). The two yield different results. Where did I commit the mistake? In the second method I have assumed that kinetic energy of the block is zero as it is slowly released, not suddenly.
2 Answers
Explanation
Your force method give you the point where the net force on the body is zero, or in other words, the equilibrium point. Whereas, the energy method gives you the point where the velocity of the block is zero. Note that $v=0\nRightarrow a=0$. In other words, zero velocity doesn't imply zero acceleration, and thus zero velocity doesn't imply zero force (because $F=ma$). So both the locations, the location of zero force/acceleration and the location of zero velocity, are different, and so you get different answers from both your methods.
Symmetry of the situation
The factor of two can be explained by the symmetric nature of the force about the equilibrium point. In this case the force is symmetric because of its linearity ($F\propto x$). So the journey from the start to the equilibrium position is just the reversed version of the journey from the equilibrium position to rest again, which implies the equilibrium point is exactly in the middle of the two extremes.
Simple Harmonic Motion
In case you're curious, the block, once left, will undergo simple harmonic motion (of course, we are neglecting resistive forces like air drag or friction) which is a special type of oscillatory motion. The following GIF gives a nice intuition of this kind of motion:
GIF Source, you can yourself try out the simulation there.
In general, when both gravity and spring force do work, conservation of mechanical energy gives: $$ K+U_{grav}+U_{spring}=k $$ However, in our case,there is also work that your hand does on the block while you try to maintain equilibrium (as the block gradually stretches the spring). And this is where your problem started. You failed to realize in this case, that your hand also contributes to the work done on the block. It's not only gravity and spring force that do work on the block while you carefully lay it down; your hand too does work on it. If we represent this work that your hand does as $W_{ other}$ then the energy equation would include this external work (generally called work done by other non-conservative forces) and the expression becomes: $$ K_1+U_{1\,grav}+ U_{1\, spring}+W_{ other}=K_2+ U_{2\, grav}+ U_{2\, spring} $$ Since both $K_1\, and\, K_2$ are zero, and taking the origin as the initial length of the spring, the equation reduces to: $$ W_{ other}=-mgh+\frac{1}{2}kh^2 $$ In truth, this is all we can write about the motion of the block if we use energy methods. We can go ahead to solve $W_{other}$ for the force you apply since we know $h$ from Hooke's law. Solving for $W_{other}$ and substituting $h=\frac{1}{k}mg$ $$ \begin{align} W_{other}&=h\left(\frac{1}{2}kh-mg\right)\\W_{other}&=h\left(-\frac{1}{2}mg\right)\\\therefore W_{other}&=-\frac{1}{2}mgh \end{align} $$ Provided the block is at equilibrium at each displacement,the work that you do is exactly half the work that gravity does and is always constant.
- 181