This question reminds you that
$$\langle 0|J^5_{\mu,0}(x)|\pi^0(p)\rangle=-if_{\pi} e^{-ipx}p_{\mu}~,$$
the mother of PCAC. That is to say, you already know this axial current corresponds to a SSB generator, and so is linear in the Goldstone boson corresponding to it,
$$
J^5_{\mu,0}\propto f_\pi \partial_\mu \pi^0 + ...
$$
where the ellipsis represents terms of higher order in the fields.
The current is basically the goldston: The corresponding charge pumps such goldstons into and out of the chirally non-invariant vacuum!
As a consequence, the corresponding term of the effective Lagrangian which gives you the above current divergence is
$$
\frac{e^2 N_c \pi^0}{48 \pi^2 f_\pi} F_{\mu\nu}\tilde{F}^{\mu\nu}.
$$
It therefore induces neutral pion decay to two photons, quite observable and physical, really.
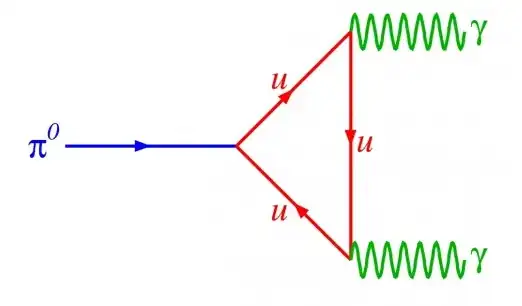
This term was an early reassurance of the genius of the WZWN term of flavor-chiral anomalous effective actions.
