I've been reading about viscoelastic models and using Excel to plot some of their characteristics. I'm particularly interested in their response to a constant strain rate which reverses periodically and goes into tension as well as compression.
I've read a number of texts that discuss the Boltzmann integral and a couple that also include the solution to the integral. Initially, I calculated the integral piece-wise in Excel and integrated it numerically. This seemed to produce a sensible force time history but, of course, is dependent on the time resolution and so looks a bit course at the strain rate turn-around.
I then used the given solution between two time limits to give me the force time history directly. A simple switching function reverses the strain rate every half a cycle and resets the start of the strain time. The problem I now have is that the function 'starts again' from zero every half cycle; it doesn't 'remember' the force at the end of the previous half. It's as if I am missing a constant of integration. Unfortunately I don't have the mathematical skills to progress any further so I wonder whether someone out there can guide me to an appropriate solution or a text that discusses this specific case?
The equation for the integral I first used is:
$$F(t)=\int_{-\infty}^tke^{-k(t-t_0)/\eta}\frac{d\varepsilon(t)}{dt}dt$$
Where the derivative is the strain rate (actually the displacement rate in my case), k is the Maxwell model spring rate, $\eta$ is its damping coefficient, and $t_0$ is the time the strain started, which I set to one quarter of a cycle in the past and which then starts from 0 every half cycle. As I say, numerically integrating this works fine.
The solution to the integral that I've obtained from another text is:
$$F(t)=\frac{d\varepsilon(t)}{dt}\frac{\eta}{k}G_0\Bigl(1-e^{-k(t-t_0)/\eta}\Bigr)$$
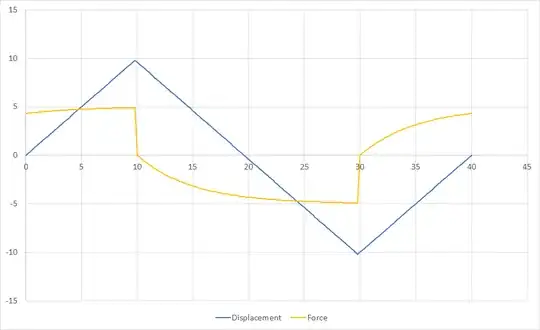
Where $G_0$ is also k and so cancels the adjacent denominator k out. It has been tricky dealing with the changes in algebraic definition and double meaning of some letters, such as $\tau$. However, as I say, the force time histories from the two methods are the same for the first quarter of a cycle, except that the first method starts from F=0 at t=0 and the second method give F=0 at t=-1/4 cycle, but that's fine and expected. The problem arises at the end of the first quarter cycle when the second method gives F=0 at t=1/4 cycle, instead of reducing from the existing force level at t=1/4 cycle, as shown in the following image.
Clearly, I could just fudge it and add the offset, but I'd rather see a proper mathematical treatment of it if possible. I'd be grateful for any clues as to how I can solve the issue.
Many thanks,
Simon.