Simple equation for repulsion force on a bounded interval

Question

I've been reading some literature on opinion dynamics models that aim to describe how agents' opinions change after interacting with each other. A classical model (from this paper) for describing how agent $n$'s opinion, denoted by $x_n(t)\in[0,1]$, moves closer to agent $m$'s opinion, denoted by $x_m(t)\in[0,1]$, is as follows:

$$x_n(t+1) = x_n(t) + \mu (x_m(t) - x_n(t))$$

where $\mu$ is a parameter assumed to be in $[0,1/2]$.

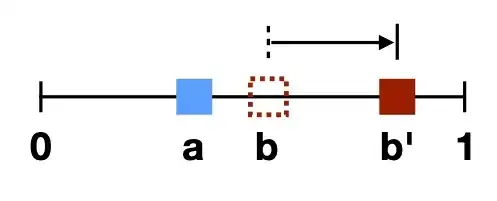
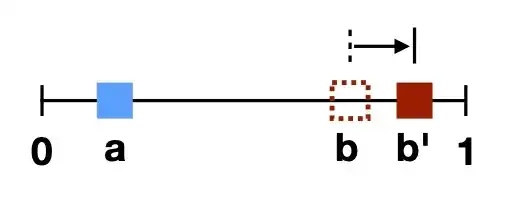
I am trying to find a simple analogous equation describing a repulsion force between two agents. To help with this derivation, I have drawn a physical analogy describing the qualitative interaction between two objects that I am seeking. Consider a fixed object (the blue block) at position $a$ and a movable red block initially at position $b$.

The repulsion equation should capture the qualitative behavior depicted in the following two figures.

In particular, in the first figure, note that when the two blocks are close together, the red block which is pushed to $b'$, far from its initial position $b$. In the second figure, when the two blocks are initially far apart, the red block only moves slightly, from $b$ to $b'$. Note that the updated position of the red block needs to remain within the bounded interval (i.e., less than $1$).

Question: What is a simple equation, analogous to the attraction equation above, for describing the repulsion between two objects on a bounded interval?

Answer 1

Let $F(r)$ be any function satisfying the following properties:

• $F(r)$ is well defined for $r\in[0,1]$.
• $F(r)\geq 0$ for $r\in[0,1]$.
• $F(r)$ is decreasing for $r\in[0,1]$.

Then a repulsive interaction satisfying your conditions can be built as follows:

For two agents $a$ and $b$, their positions at time $t_{i+1}$ are determined from their positions at time $t_i$ as follows:

$$a(t_{i+1})=g\bigg(a(t_i)+\text{sgn}\big(a(t_i)-b(t_i)\big)F\big(|a(t_i)-b(t_i)|\big)\bigg)$$ $$b(t_{i+1})=g\bigg(b(t_i)+\text{sgn}\big(b(t_i)-a(t_i)\big)F\big(|a(t_i)-b(t_i)|\big)\bigg)$$

where

$$\text{sgn}(x)=\begin{cases}1 & \text{if }x>0 \\ 0 & \text{if }x=0 \\ -1 & \text{if }x<0\end{cases}$$

is the usual "sign function", and

$$g(x)=\begin{cases}0 & \text{if }x<0\\x&\text{if }0\leq x\leq 1\\1&\text{if }x>1\end{cases}$$

is a "limiter" function. The sign function ensures that the force is pointing the right direction to be repulsive, and the $g$ function ensures that the results always fall in the unit interval.

There are an infinity of possible choices for $F$; examples include:

• $F(r)=\mu(1-r)$
• $F(r)=\mu(1-r^n)$
• $F(r)=\frac{\mu}{r+\epsilon}$
• $F(r)=e^{-\mu r}$

Answer 2

Another option. If you define:

$f(x)=\begin{cases}-1-x & \text{if }x<0 \\ 1-x &\text{if }x>0\end{cases}$

and

$g(x)=\begin{cases}0 & \text{if }x \le -1 \\ x & \text{if }-1<x<1 \\ 1 & \text{if }x\ge1\end{cases}$

Then you can use:

$x_b(t+1)=g[x_b(t)+\mu f(x_b(t)-x_a(t))]$

$f$ gives the interaction, which decreases linearly with distance, and $g$ makes sure the result is in the interval [0,1]

Answer 3

One simple possibility would be $$x_n(t+1)=x_n(t)-\mu\cdot\text{ sgn}(x_m(t)-x_n(t))\cdot|x_m(t)-x_n(t)|^{-\gamma}\cdot x_n(t)\cdot (1-x_n(t))$$

• The minus sign before $\mu$ makes the interaction repulsive.
• $\gamma$ makes the repulsion smaller as the agents get further away if $\gamma>1$.
• The $x_n(t)$ makes the repulsion smaller as $x_n$ becomes closer to the left boundary
• The $(1-x_n(t))$ term makes the repulsion smaller as $x_n$ becomes closer to the right boundary
• Since the agents are always in the interval [0,1] the signs of $x_n,(1-x_n)$ are always correct
• A different range of $\mu$ would have to be chosen to account for these additional factors

This force becomes larger in the middle $x_n\approx 1/2$ which is hard to avoid when you want to keep the agents inside [0,1]. You can take different powers of $x_n, (1-x_n)$ to make this effect less noticable. For example $x_n^{1/4}$ and $(1-x_n)^{1/4}$ where 4 could be any number.

---

EDIT I replaced $(x_m(t)-x_n(t))^{-\gamma}$ with $\text{sgn}(x_m(t)-x_n(t))\cdot |x_m(t)-x_n(t)|^{-\gamma}$, making my answer closing to the other answers. The old term won't work for negative numbers. Sadly 'simple' is a bit of a stretch now.