Answered:
... can we say that for objects with a constant charge density that their charge can be assumed to be concentrated at their geometric centres?
The answer is no.
A good rule of thumb in understanding these kind of things intuitively is "what you see is what you feel": imagine you are a little tiny you and can inhabit any point in the space. You have around you a spherical field of view, or "view sphere". If, in that field of view, you can "see" something charged that looks like a point (i.e. it occupies a small angular size thereupon), you will feel the force from a point charge, even if it's not really a point charge. If you "see" a plane of charge stretching to your horizon, you will feel force like a plane charge, even if it's not actually a plane. And so forth.
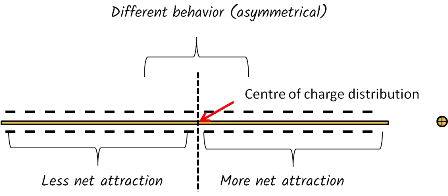
Now in your scenario, when you are near the center of charge of your situation, you don't see a charge there, so the effect of that center point is it has no effect: but you do "see" two charges on either side, and so you will feel influence from them as such.
Alternatively, one can think of this from the "third person" or test charge perspective: note that exactly at the center point between your two charges, the force on a test charge will be zero because the force from both exactly balance. Note also that this center point is the center of charge, if both are equal. Now consider a point just slightly off from it. By continuity, the force will be small, but not zero. In fact, for a time, it will grow as you move away from that center, and so away from the center of charge, which is emphatically not the behavior if you are talking about being close to a simple point charge. Hence the center of charge is not a point charge equal to the other two charges.
That said, if you are very far from the distribution, then you can, indeed, treat it as approximately a point charge: however, in this case, the distinction between "center of charge" and other "centers" also approximately disappears - you "see" both charges as being a single point in your field of view.
Also, I believe the above idea of "what you see is what you feel" can be made mathematically rigorous as actually exact, though I have not gone through the derivations to be sure, but it should be because the field around a charge looks just like the emanation of rays of light (as in geometric optics, not as in actual light waves in the EM field - think of the "field lines") therefrom, with intensity or surface brightness proportional to the charge. Hence the same mathematical rules that apply to the emanation and vision of light, will also apply to electric force (and also gravitational force, too, at least below the general-relativistic regime).