You are asking about the algebra of angular velocities, especially as it relates to the area of kinematics.
Consider the tea-cup ride at Disney. You have a platter (orange) rotating about A with angular speed $\Omega$. At some radius $R$ away form the center a 2nd object (green) is pinned at point B with relative speed $\dot \theta$. This is to denote that $\theta$ is an orientation angle. On this object there are two attached points, C and D, that at some instance in time are located as shown below:
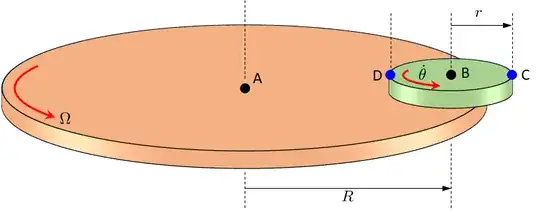
What is the rotational velocity of A?
Every particle attached to the platter moves with translational velocity except the center of rotation. Nevertheless we can state that the body rotates with $\Omega$ and the translational speed of each particles is given by $$ v= R\, \Omega $$ where $R$ is the radial distance from the center of rotation. You can say that B rotates about A, but in reality the entire body is rotating about A. A more accurate description would be that B orbits A.
What is the rotational velocity of B?
This depends on which body is B belong to. The bottom of the pin connecting the two bodies rotates with $\Omega$ and the top of the pin with $$\omega = \Omega + \dot\theta$$ since $\dot \theta$ is the relative motion between the two bodies.
What is the translational velocity of points A, B, C and D.
$v_A = 0$
since it is on a fixed point
$v_B = R\,\Omega$
as we saw before
$v_C = v_B + \omega \, r = \Omega \,R + (\Omega + \dot \theta) \, r = \Omega ( R+r) + \dot \theta \, r $
To be interpreted as the velocity of the platter at C plus the relative velocity of the second body.
$v_D = v_B - \omega \, r = \Omega \,R - (\Omega + \dot \theta) \, r = \Omega ( R-r) - \dot \theta \, r $
To be interpreted as the velocity of the platter at C minus the relative velocity of the second body.
As you can see, relative translational velocities switch signs between C and D. This is because the position of the point is either radially out or radially in from the reference point B.
On the contrary rotational velocity of the second body is only added the motion of the platter, because the location of the pin at B bears no significance in the rotational kinematics.