In plasma physics, what Debye length should represent in practice?
From what I understood it's the maximum characteristic distance within which separate charges can be present in the internal space of an overall neutral plasma, due to the presence of potential and thermal energy.
But what happen over this distance? how can I visualize it graphically?
To understand the meaning of Debye length, one should derive it. There are several ways to derive Debye length. Here I try to sketch the simplest of them.
Consider the charge $q$. If it is alone, it produces potential $\phi_0=q/r$. Presence of other particles in plasma change this potential. For simplicity, let us consider that thera two species in plasma with charge number $Z=1$. Their equilibrium distributions are $$n_i=n\exp(-e\phi/(k_BT)),\quad n_e=n\exp(+e\phi/(k_BT)).$$ The potential $\phi$ obeys Poisson equation, $$\Delta\phi=-4\pi\rho,$$ where $\rho$ is volume charge density, $$\rho=en\left[\exp(-e\phi/(k_BT))-\exp(+e\phi/(k_BT))\right]$$ For small enough potential $\phi$, density is $\rho\approx -2ne\phi/(k_BT)$. Keeping in mind spherical symmetry of probe charge potential, we solve the equation, $$\Delta \phi=\frac{8\pi ne^2}{k_BT}\phi$$ and find that $$\phi=\frac{C}{r}e^{-r/r_D},\quad r_D^2=\frac{k_BT}{8\pi ne^2}.$$ In the limit of small distances $\phi$ should go into $\phi_0$ (the probe charge does not know about other charges in system), so $$\phi=\frac{q}{r}e^{-r/r_D}.$$ The obtained result means that for distances $r/r_D\gg 1$ two charges in plasma do not interact by Coulomb. Also, it means that if one try to ''measure'' the charge of particle in plasma, he obtain the smaller value.
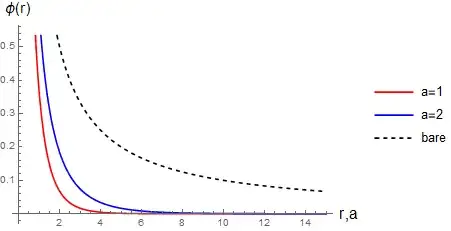
To visualize it, we can plot bare potential (without Debye screening) and scereened potential,
